BERECHNUNG STROMUNGSPROBLEM auf DIRMU - Bernard Couapel

BERECHNUNG ZWEIDIMENSIONALER STROMUNGSPROBLEME AUF EINEM DIRMU-MULTIPROZESSOR-RING

Von

B. Couapel*, G. Scheuerer**, J. Volkert***

LSTM-Bericht 189/T/87

Juli 1987

Version PDF

 

* Institut de Formation Supérieure en

Informatique et Communication

Université de Rennes I

Avenue du Général Leclerc

F—35042 Rennes

** Lehrstuhl für Strömungsmechanik

Universität Erlanqen-Nürnberg

Egerlandstr. 13

D—8520 Erlangen

*** Institut für Mathematische Maschinen

und Datenverarbeitung III

Universität Erlangen-NUrnberq

Martensstr. 3

D—8520 Erlanqen

 

Zusammenfassung

In der Arbeit wird die Implementation einer Finite-VolumenMethode zur Lösung der Navier-Stokes-Gleichungen auf dem DIRMU-Multiprozessor-System beschrieben. Als Testfall wird die laminare, inkompressible Strömung über eine rückwärts springende Stufe betrachtet, für die Vergleichslösungen auf einem seriellen Rechner vorliegen. Das Rechenverfahren verwendet den sog. SIMPLE-Algorithmus, bei dem iterativ lineare Gleichungssysteme für die beiden Geschwindigkeitskomponenten und eine Druckkorrektur gelöst werden, bis die Massen- und Impulserhaltungsgleichungen simultan erfüllt sind.

Als Rechnerkonfiguration wird ein Prozessorring verwendet; das Rechengebiet wird dabei in einzelne Streifen unterteilt. Jeder Prozessor bearbeitet einen solchen Streifen. Theoretisch läßt sich mit einer solchen Anordnung ein zur Anzahl der Prozessoren direkt proportionaler Speedup erreichen. Die im Rahmen dieser Arbeit durchgeführten Messungen zeigen, daß diese theoretischen Werte bei feinen numerischen Gittern nahezu erreicht werden. Die Verluste durch Kommunikation zwischen den Prozessoren betragen, je nach Rechengitter und Anzahl der Prozessoren, 5-20 %. Verbesserungen des parallelisierten Verfahrens müssen vor allem den Lösungsalgorithmus für die linearen Gleichungssystem betreffen. In dieser Arbeit wurde eine linieninterative Methode eingesetzt; zukünftig soll verstärkt die Parallelisierungsmöglichkeiten effizienterer Algorithmen untersucht werden.

 

Vorwort

Die vorliegende Arbeit entstand im Rahmen des von der Stiftung Volkswagenwerk geförderten Forschungsvorhabens "Lösungen strömungsmechanischer Grundgleichungen unter Berücksichtung moderner Rechnerstrukturen".

Die Autoren bedanken sich bei Prof. Dr. W. Händler, Prof. Dr. A. Bode und Prof. Dr. F. Durst für ihre Unterstützung und ihr konstantes Interesse an der Arbeit. Frau Dipl.-Ing. M. Barcus, Herrn Dr. M. Peric sowie Herrn Prof. Dr. J. H. Ferziger sei für die zahlreichen Diskussionen und für die Mithilfe bei der Fertigstellung der Arbeit gedankt.

 

1. Einleitung

 

1.1. Problemstellung

Moderne Verfahren zur Strömungsberechnung bauen auf einer numerischen Lösung der Navier-Stokes-Gleichungen auf. Im laminaren Fall, d.h. bei kleinen Reynoldszahlen, werden diese direkt gelöst. Für die technisch relevanten turbulenten Strömungen werden i.a. gemittelte Formen dieser Gleichungen in Verbindung mit einem Turbulenzmodell betrachtet (Bradshaw et al., 1981). Bei beiden Strömungsarten muß jeweils ein System aus nichtlinearen, miteinander gekoppelten, partiellen Differentialgleichungen 2. Ordnung integriert werden. Für Strömungen mit Rezirkulation erfordert dessen Lösung bereits für zweidimensionale Geometrien einen erheblichen Aufwand an Computer-Rechenzeit und Speicherplatz. Für die praktisch interessierenden dreidimensionalen Strömungen sind diese Anforderungen noch wesentlich höher. Zur Strömungsberechnung um vollständige technische Konfigurationen, wie z.B. Flug- oder Fahrzeuge, sind Rechnerspeicher mit mehr als 10⁹ Worten und Rechenleistungen im Bereich von GFlops notwendig.

Wegen dieser hohen Anforderungen nimmt vor allem in den U.S.A. die Strömungsmechanik eine treibende Rolle in der Entwicklung von Hochleistungsrechnern ein (Kutler, 1985). Bis vor kurzem handelte es sich bei diesen hauptsächlich um Vektorrechner mit technologisch hochwertigen Prozessoren, aber einem geringen Grad an Nebenläufigkeit bzw. Parallelität. In den letzten Jahren hat sich jedoch die Erkenntnis durchgesetzt, daß bedeutende Fortschritte in der Rechengeschwindigkeit und Speicherplatzkapazität mit solchen Architekturen nicht mehr zu realisieren sind. Deshalb erfolgte eine verstärkten Hinwendung auf Rechner mit einem hohen Maß an Nebenläufigkeit, sog. Parallel- oder Multiprozessoren; bei diesen bearbeiten mehrere Rechner (Prozessoren) eine Aufgabe simultan. Theoretisch können damit Rechenzeit- und Speicherplatzgewinne proportional zur Anzahl der verwendeten Prozessoren erzielt werden. Das Konzept weist zudem eine hohe Flexibilität und Erweiterbarkeit auf. Multiprozessoren bieten das Potential, große strömungsmechanische Probleme anzugehen, deren Bearbeitung mit den heute verfügbaren Rechnern nicht möglich ist.

Da die Multiprozessorentwicklung erst vor einigen Jahren begonnen hat, gibt es derzeit nur wenige, lauffähige Multiprozessoren mit großer Prozessorzahl; dementsprechend noch geringer sind deren Anwendungen mit strömungsmechanischen Bezug. Der derzeitige Stand der Forschung auf diesem Gebiet wird im nächsten Abschnitt beschrieben.

 

1.2. Stand der Forschung

Seit einigen Jahren sind Multiprozessoren mit geringer Prozessorzahl Stand der Technik und kommerziell erhältlich. Typisch sind derzeit Systeme mit 2 - 4 Prozessoren. Solche Multiprozessoren werden im kommerziellen Bereich zur Erhöhung des Durchsatzes verwendet (Z.B. IBM 3801). Auch auf dem Gebiet der wissenschaftlichen Hochleistungsrechner ist ein Trend zu Mehrprozessorsystemen feststellbar (z.B. CRAY-XMP, CRAY 2, ETA 10).

Anlagen mit höherer Prozessorzahl, die kommerziell vertrieben werden, besitzen meist relativ schwache Verbindungen zwischen den einzelnen Elementen. Ein Beispiel ist der ALLIANT-Rechner mit 8 Prozessoren an einem einzigen Bus. Eine Ausnahme bilden die verschiedenen Realisationen des Hypercube, die seit neuestem auf dem Markt erhältlich sind und bei denen es Verbindungssysteme für 2ⁿ Prozessoren gibt. Multiprozessoren mit Verbindungsnetzwerken, die eine weit größere Bandbreite zur Verfügung stellen (Speicherkopplung über Multiportspeicher oder über mehrstufige Netzwerke) sind derzeit nur in Forschungseinrichtungen zu finden.

Am Institut für Mathematische Maschinen und Datenverarbeitung (IMMD) der Universität Erlangen-Nürnberg werden seit Mitte der 70er Jahre über Multiportspeicher gekoppelte Systeme untersucht. Im Augenblick steht der Multiprozessorbaukasten DIRMU25 (Händler et al., 1985) zur Verfügung. Aus den einzelnen Bauelementen, die je aus einem Prozessor, Coprozessor und Speicher bestehen, lassen sich verschiedenartige Architekturen mit bis zu 26 Prozessoren einfach konfigurieren (Z.B. Ringe, Felder, Hypercubes usw.). Das System dient zur Entwicklung und Bewertung paralleler Strukturen und paralleler Anwenderprogramme.

Damit wurden bereits einige strömungsmechanische bzw. dazu verwandte Aufgaben erfolgreich bearbeitet. Beispiele sind die Lösung der Poisson-Gleichung mit einem Finite-Differenzen-Verfahren und der Gauß-Seidel-Methode als Lösungsalgorithmus (Händler et al., 1985) sowie die Lösung der Stokes-Gleichungen mit einer Mehrgittermethode (Geus, 1985). In beiden Fällen konnten nahezu linear mit der Anzahl der verwendeten Prozessoren abnehmende Rechenzeiten gemessen werden.

Im Rahmen des SUPRENUM-Projektes des Bundesministeriums für Forschung und Technologie hat Thole (1985) die drei-dimensionale Poisson-Gleichung auf einem Hypercube-Rechner bearbeitet. Die Prozessoren waren in Form eines aus bis zu 32 Elementen bestehenden Feldes angeordnet. Zur Lösung wurde ein Mehrgitterverfahren mit V-Zyklen verwendet. Wegen der in der Arbeit verwendeten relativ groben Gitter und dem damit verbundenen hohen Anteil an Kommunikationszeiten, wurden Rechenzeitersparnisse nur in der Größenordnung von 50% gemessen.

 

1.3. Ziele der Arbeit

In dieser Arbeit wird die Anwendung von DIRMU-25 zur numerischen Lösung der Navier-Stokes-Gleichungen mit einer Finite-Volumen-Methode beschrieben. Als Testfall dient die zweidimensionale, laminare, inkompressible Strömung über eine rückwärts springende Stufe. Die parallelisierte Version des Rechenverfahrens soll durch den Vergleich der Ergebnisse mit denen einer seriellen Version verifiziert werden. Das Ziel der Untersuchungen ist, durch Messungen herauszufinden, welche Rechenzeitersparnisse sich bei Strömungsberechnungen durch den Einsatz von Multiprozessoren ergeben; gleichzeitig sollen mögliche Schwachpunkte und Probleme bei der parallelen Implementierung aufgezeigt und Lösungsvorschläge erarbeitet werden.

 

1.4. Inhalt der Arbeit

In Kapitel 2 wird die behandelte Geometrie und das zu lösende Gleichungssystem mit den entsprechenden Randbedingungen beschrieben. Daran schließt sich in Kapitel 3 eine ausführliche Diskussion der für die Berechnungen verwendeten Finite-Volumen-Methode an. Kapitel 4 ist dem DIRMU-25 Multiprozessorsystem gewidmet: das Grundkonzept sowie die Hard- und Software-Komponenten dieses Rechners werden erläutert. In Kapitel 5 wird die parallele Implementierung der numerischen Methode vorgestellt. In den Abschnitten 5.1 und 5.2 wird die verwendete Rechnerkonfiguration und die Aufteilung der Variablenfelder beschrieben. Der Ablauf des parallelisierten Verfahrens wird in Abschnitt 5.3 besprochen. Abschnitt 5.4 behandelt den wichtigen Aspekt der Synchronisierung der einzelnen Rechner. Die Ergebnisse werden in Kapitel 6 in Form von Tabellen und Diagrammen gezeigt und kritisch diskutiert. Die Schlußfolgerungen befinden sich im abschließenden Kapitel 7.

 

2. Mathematisches Modell

 

2.1. Geometrie und Koordinatensystem

Abb. 2.1 zeigt die Geometrie und das Koordinatensystem des betrachteten Testbeispieles: der zweidimensionalen, laminaren Strömung über eine rückwärtsspringende Stufe. Das Integrationsgebiet besitzt die Länge L = 0.25 m; die Höhe des Kanales am Austritt ist H = 0.05 m. Die Stufenhöhe beträgt h = H/2.

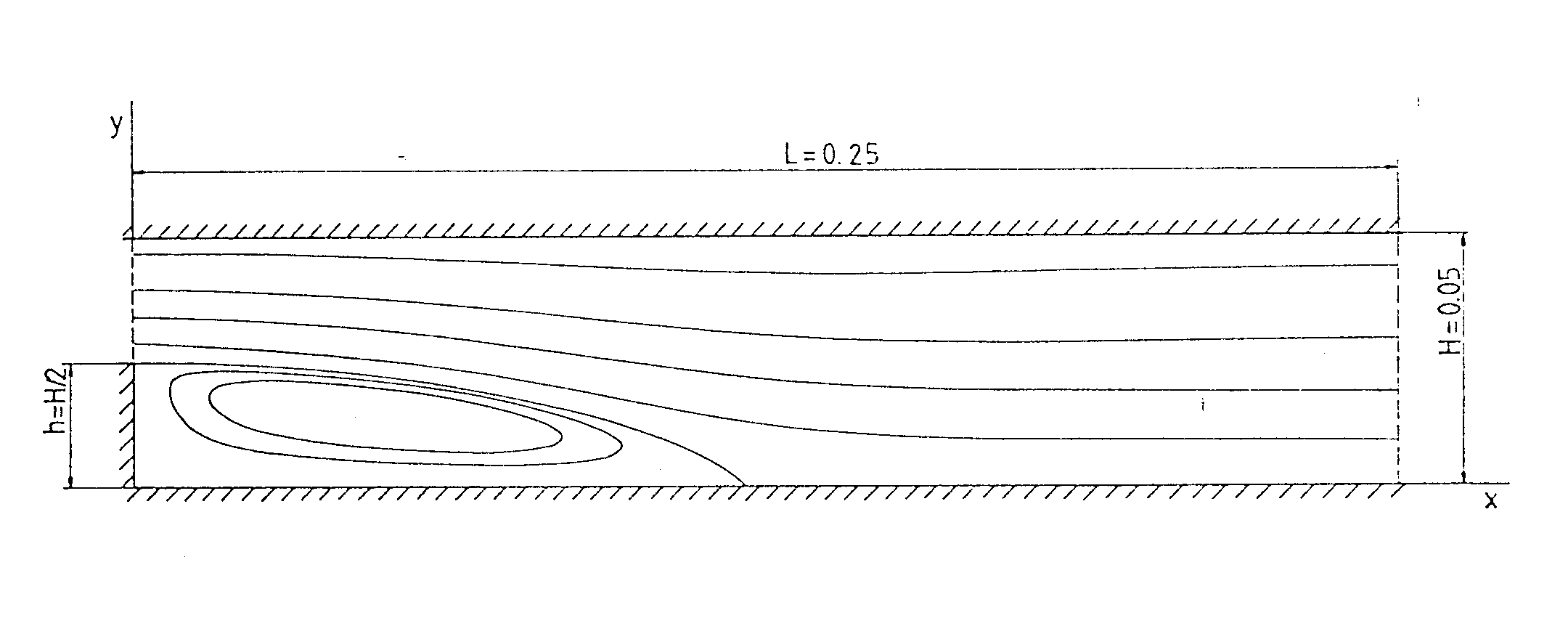
Abb. 2.1 Geometrie des Testfalles und Koordinatensystem

 

2.2. Navier-Stokes-Gleichungen

Die in Abb. 2.1 gezeigte Strömung läßt sich durch die physikalischen Erhaltungssätze für Masse und Impuls beschreiben. Unter der Annahme stationärer, zweidimensionaler, laminarer und dichtebeständiger Strömung lauten diese für ein Newton‘sches Fluid (Bird et al., 1960):

Massenerhaltung:

Erhaltung von x—Impuls:

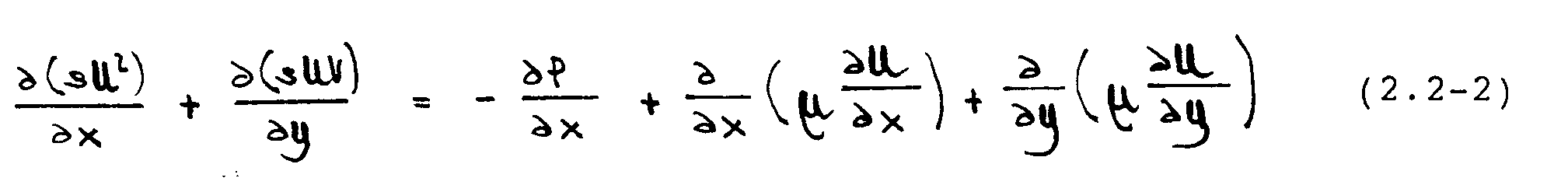
Erhaltung von y-Impuls:

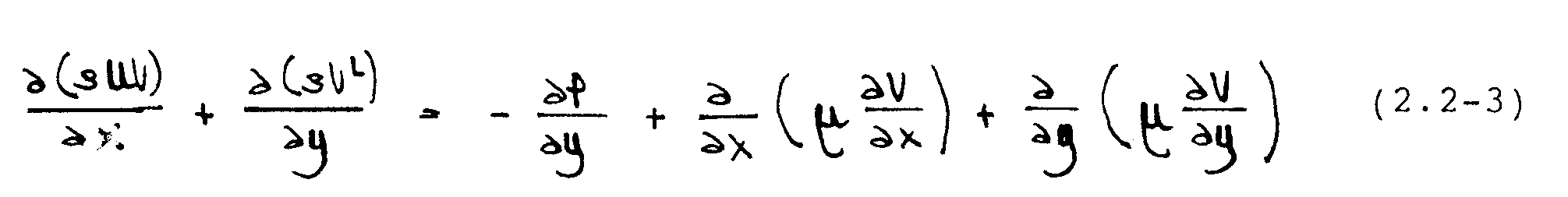
In diesen Gleichungen stellen U und V die Geschwindigkeiten in der x- bzw. y-Richtung dar; P ist der statische Druck. Die Größen -Á und -¼ bezeichnen die Dichte und dynamische Viskosität des Fluids.

Die Gleichungen (2.2-1) - (2.2-3) werden als Navier-Stokes-Gleichungen bezeichnet. Sie bilden ein gekoppeltes System aus elliptischen, partiellen Differentialgleichungen. Für eine eindeutige Lösung sind Randbedingungen entlang aller Ränder des Integrationsgebietes notwendig; diese werden im nächsten Abschnitt angegeben.

 

2.3. Randbedingungen

Die Ränder des in Abb. 2.1 gezeigten Integrationsgebietes werden von Wänden, einem Einström- und einem Ausströmrand gebildet. Die notwendigen Randbedingungen werden in dieser Reihenfolge diskutiert.

An den Wänden gilt die Haftbedingung. Die Geschwindigkeiten werden dort zu Null gesetzt, gemäß

Am Einströmrand wird eine voll entwickelte Kanalströmung mit einem parabolischen Geschwindigkeitsprofil nach der Beziehung

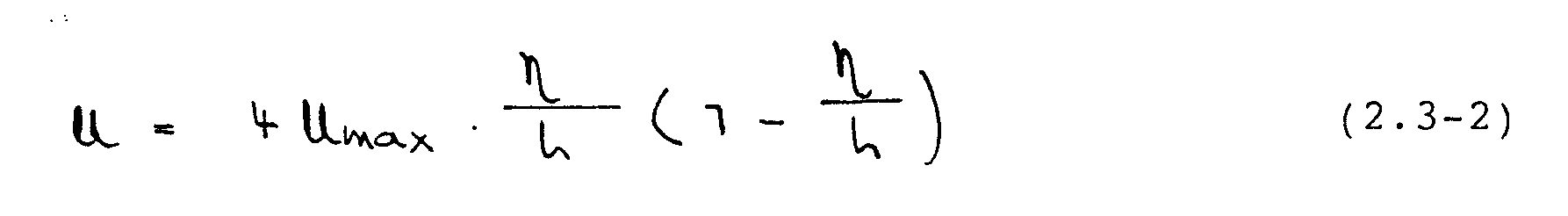
angenommen, wobei der Koordinatenursprung von -· an der Stufe ist. Die Normalgeschwindigkeit V wird am Einstromrand zu Null gesetzt. Mit den hier gewählten Werten von U_max = 1.5 m/s, = 1 kg/m³ und -¼= .00375 Das ergibt sich eine Reynoldszahl

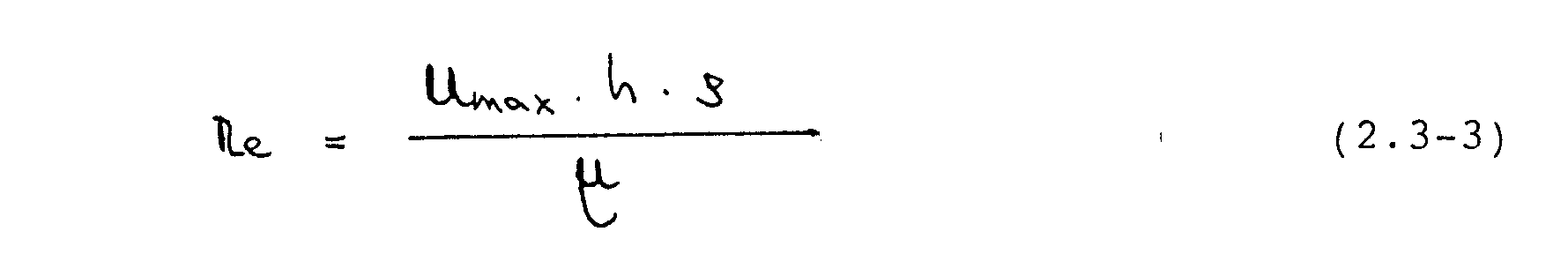
von 100.

Am Auströmrand, der sich in ausreichender Entfernung vom Rückströmgebiet befinden muß, werden vernachlässigbare Anderungen der U- und V-Geschwindigkeiten in der x-Richtung vorausgesetzt:

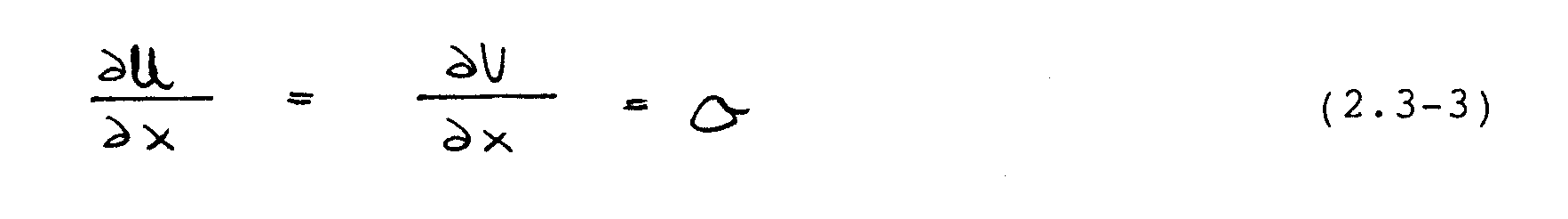
Mit Hilfe der angegebenen Beziehungen sind die in Abschnitt 2.2 beschriebenen Navier-Stokes-Gleichungen eindeutig bestimmt.

 

3. Numerisches Lösungsverfahren

Zur numerischen Lösung der Navier—Stokes-Gleichungen wird die von Peric und Scheuerer (1987) beschriebene konservative Finite-Volumen-Methode CAST verwendet. Die wesentlichen Elemente dieses Verfahrens sind die

- Diskretisierung des Lösungsgebietes (Kontrollvolumenanordnung), die

- Diskretisierung der Erhaltungsgleichungen und die

- Algorithmen zur Lösung der entstehenden, linearen Differenzengleichungssysteme.

Sie werden in den folgenden Abschnitten in dieser Reihenfolge diskutiert.

 

3.1. Kontrollvolumenanordnung

In Finite-Volumen-Verfahren wird das Integrationsgebiet in eine endliche Anzahl von Kontrollvolumen aufgeteilt. Die Gitterpunkte liegen jeweils im Schwerpunkt der Kontrollvolumen, s. Abb. 3.1. Bis vor kurzem wurden zur Lösung der Navier-StokesGleichungen fast ausschließlich versetzte Kontrollvolumenanordnungen (staggered grids) verwendet (Patankar, 1980). Dieser Ansatz wird auch in der vorliegenden Arbeit gewählt.

Die U- und V-Geschwindigkeiten werden, wie in Abb. 3.1 gezeigt, versetzt zum Druck P im Integrationsgebiet gespeichert. Die Stützstellen der U-Geschwindigkeiten liegen an den Grenzflächen der Druckkontrollvolumen mit x = const. und die der V-Geschwindigkeiten an den entsprechenden Stellen mit y = const. Der Vorteil dieser Anordnung ist, daß keine oszillatorischen Druckfelder entstehen können. Dieser Punkt wird im Detail von Patankar (1980) diskutiert.

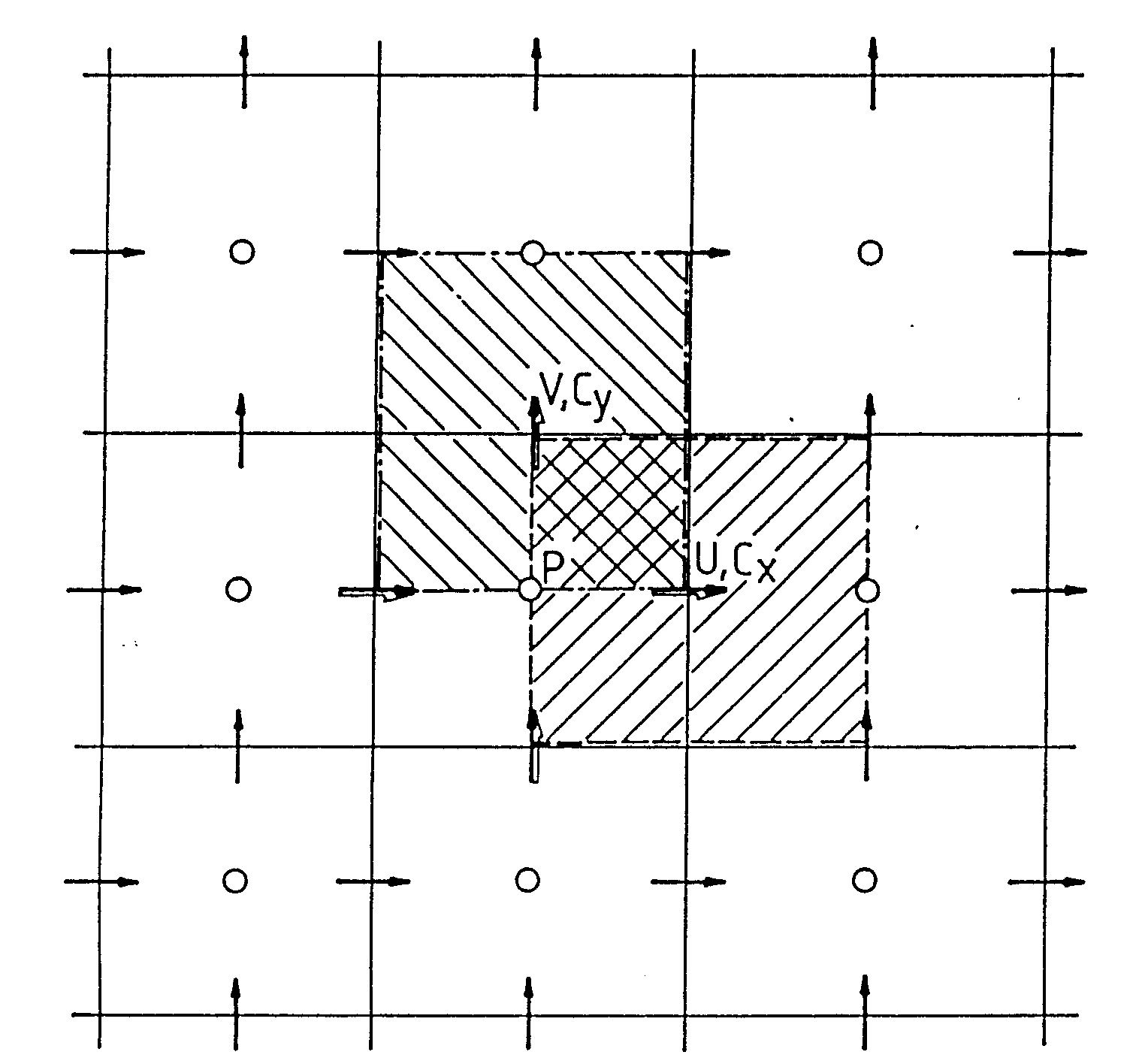
Abb.3.1: Kontrollvolumenanordnung beim versetzen Gitter

 

3.2. Finite-Volumen-Diskretisierung

Die Diskretisierung wird anhand der folgenden verallgemeinerten TranspOrtgleichUflg erläutert:

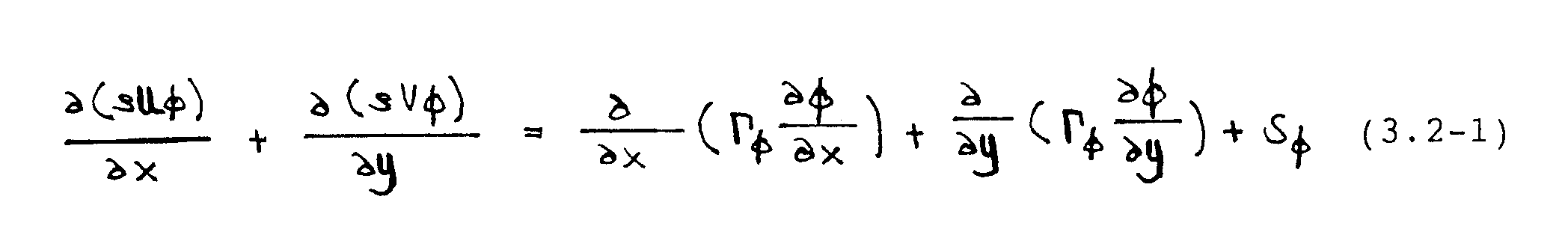
Im Falle der U-Gleichung gilt -¦ = U und 5 = - -´P/-´x. Die V-Gleichung kann analog gebildet werden. Gleichung (3.2-1) wird formal -Ìber ein Kontrollvolumen integriert, wobei die Volumenintegrale auf der linken Seite mit Hilfe des Satz von Gauß in Oberflächenintegrale umgeformt werden. Mit Bezug auf Abbildung 3.2 folgt

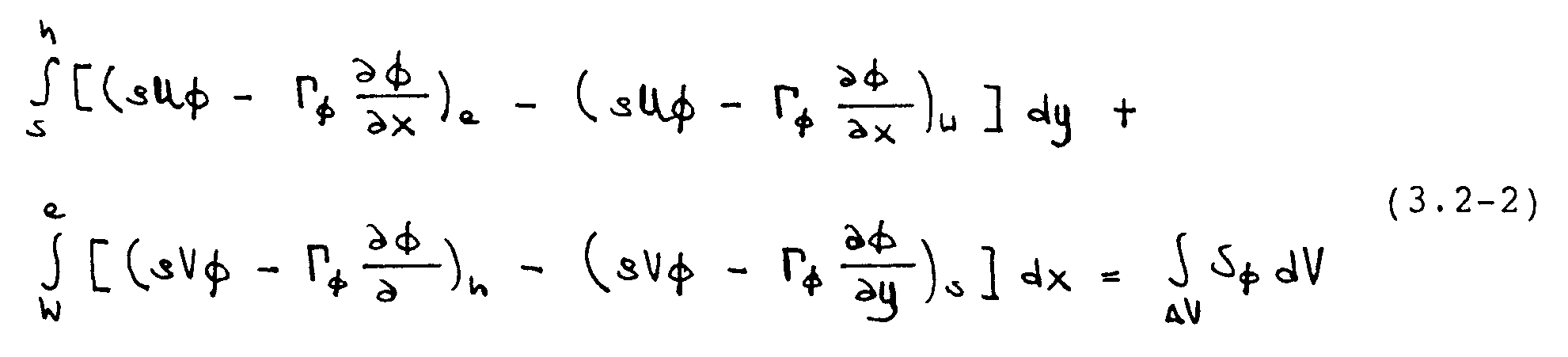
Diese Integro-Differentialgleichung ist gleichwertig mit der Ausgangsgleichung (3.2-1). Sie stellt ein Gleichgewicht der über die Kontrollvolumengrenzflächen ein- bzw. austretenden konvektiven und diffusiven Flüße und der im Kontrollvolumen befindlichen Quellterme dar. In Finite-Volumen-Verfahren wird Gleichung (3.2-2) anstelle von (3.2-1) approximiert. Dies ergibt eine konservative Diskretisierung, bei der keine numerischen Verluste von Masse und Impuls auftreten können.

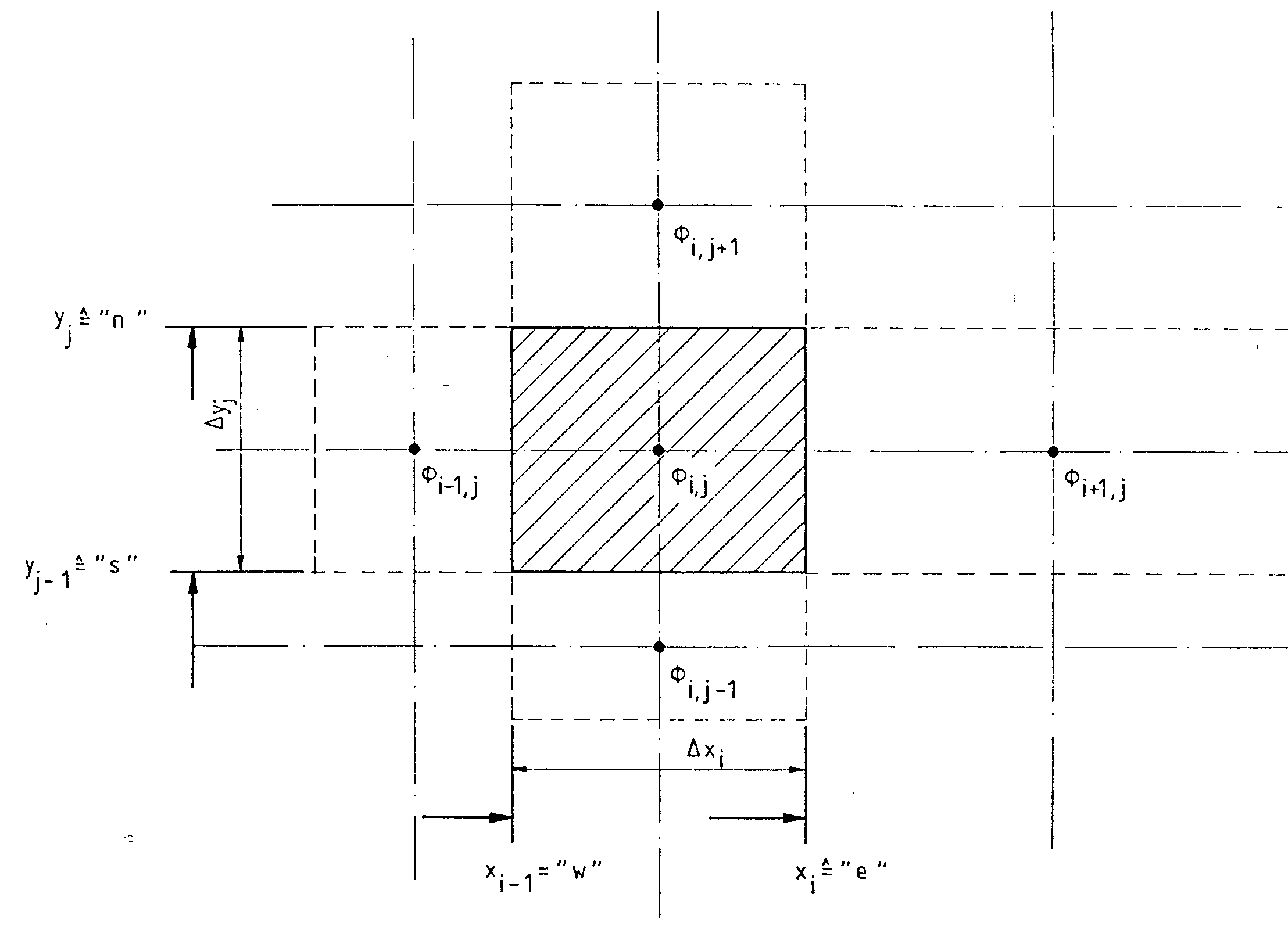Abb. 3.2 Geometrie eines Kontrollvolumens

Im ersten Approximationsschritt werden die Integrale in Gleichung (3.2-2) ausgewertet und die Gleichung linearisiert. Die dabei getroffenen Annahmen sind

- die Flüsse entlang der Kontrollvolumengrenzflächefl und

- die Quellterme im Kontrollvolumen sind konstant.

Zur Linearisierung der Beziehung werden die Massenströme C_x = -ÁU und C_y = -ÁV jeweils mit Werten vom vorhergehenden Iterationsschritt berechnet. Es ergibt sich der folgende Ausdruck

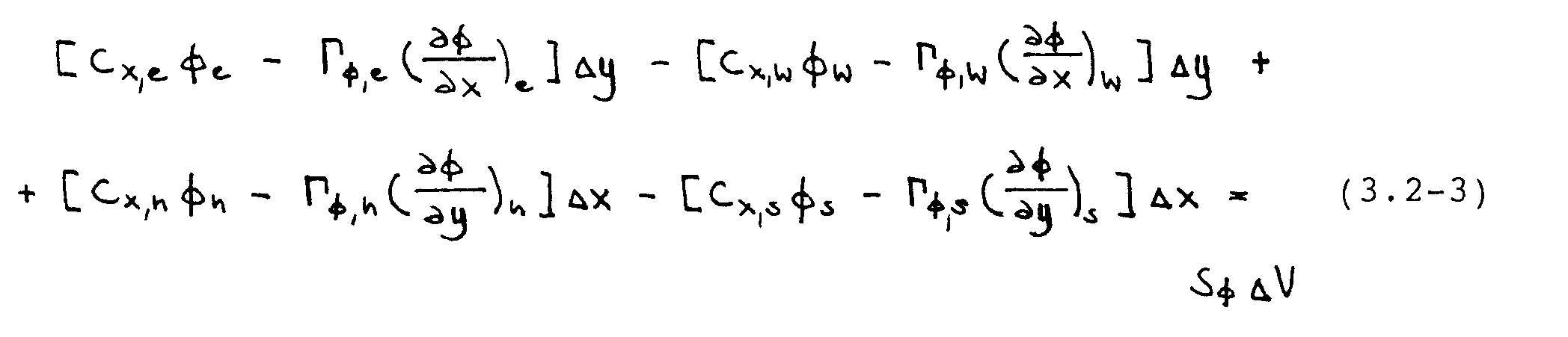
Der zweite Approximationsschritt besteht darin, die Funktionswerte ^4~e‘ 4~.7, #~n, 4~ und die entsprechenden Gradienten an den Kontrollvolumengrenzflächen in Abhängigkeit von den Gitterpunktwerten auszudrücken. Für die ersteren wird das sog. Upwind-Verfahrefl (s. Patankar, 1980) benutzt. Die exakte ~-Verteilung wird gemäß Abb. 3.3 durch eine Treppenfunktion angenähert, wobei jeweils die Richtung des Massenstromes mitbetrachtet wird. Für den Wert 4y in Abb. 3.3 gilt z.B.

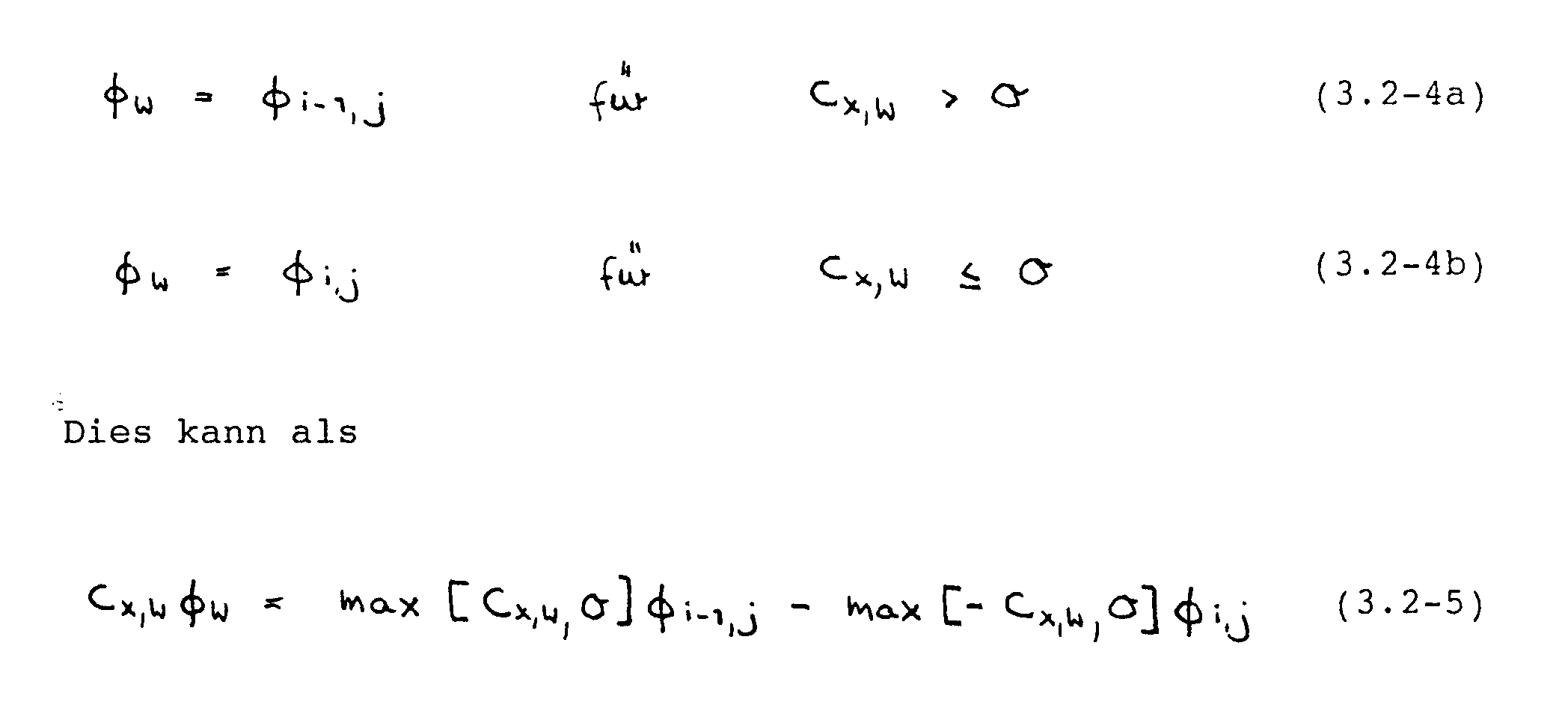geschrieben werden, wobei max [a,b] den größeren Wert von a und b bedeutet. Die Massenströme Cx,m mit m = w,e,n,s werden durch lineare Interpolation aus den Gitterpunktwerten ermittelt.

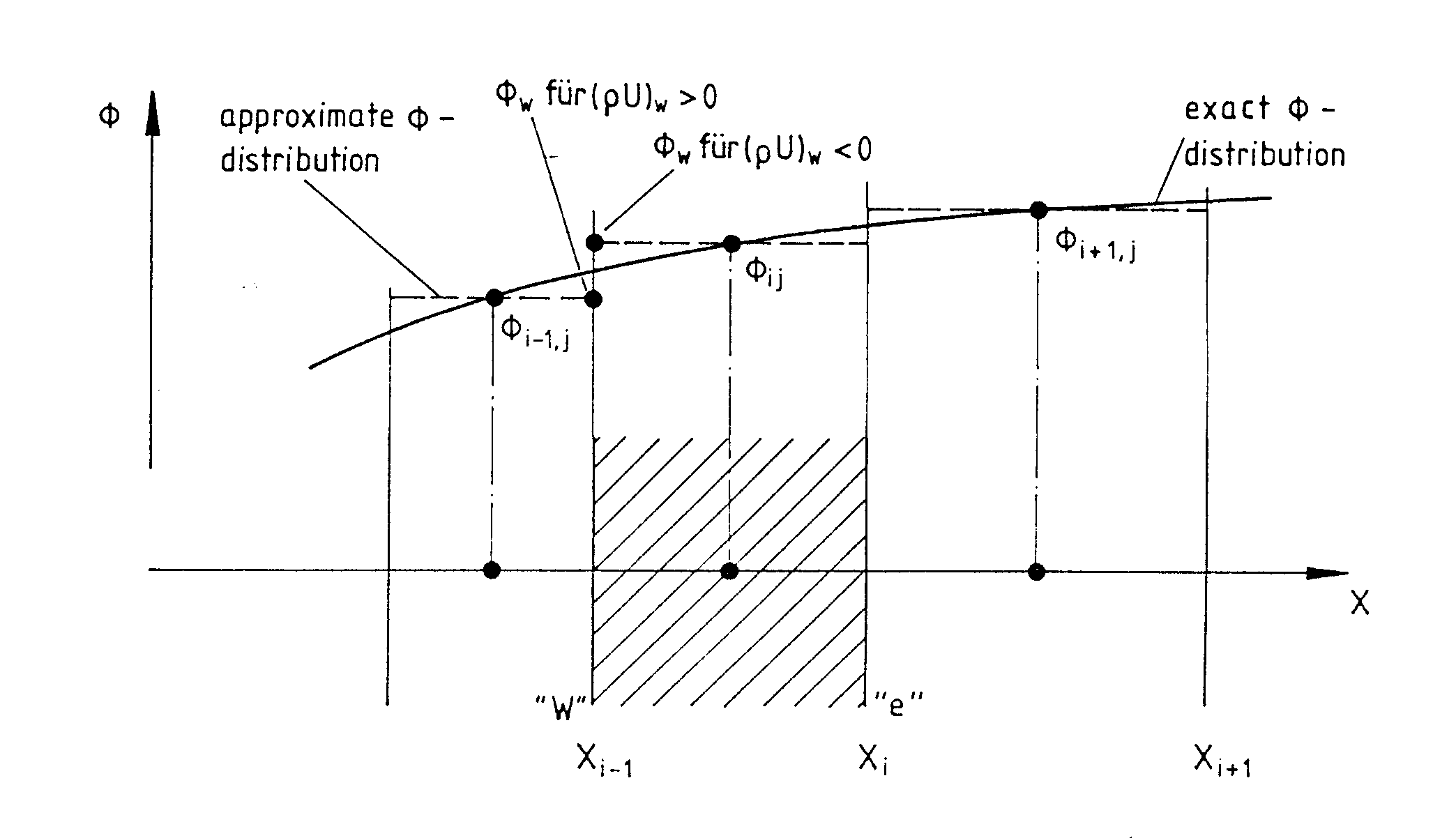
Abb. 3.3 : Upwind—Approximation der Konvektionsterme

Für die Gradienten (-´-¦/-´x)e, (-´-¦/-´x)w, etc. werden Zentral-differenzen verwendet, d.h. die exakte {-verteilung wird durch Geraden angenähert. Nach Abb. 3.4 gilt

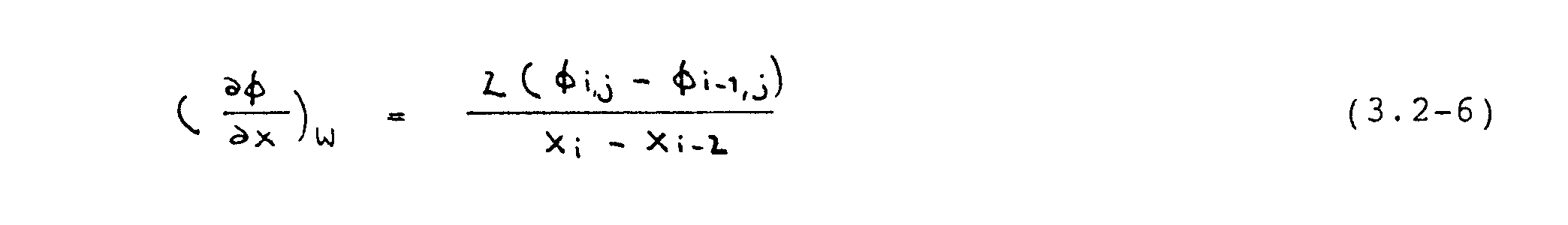
mit entsprechenden Ausdrücken für die weiteren Gradienten in Gleichung (3.2-3).

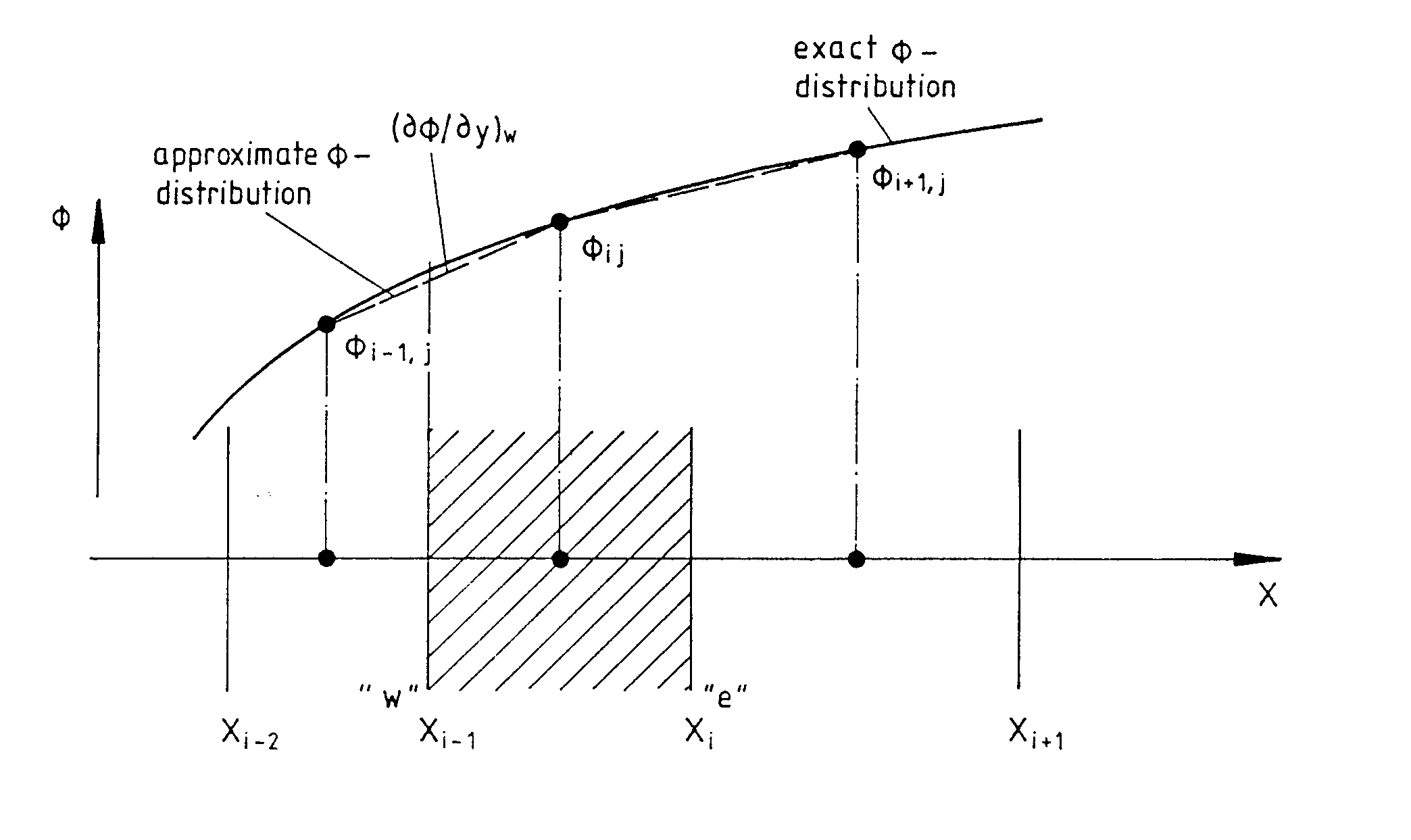
Abb. 3.4 : Zentraldifferenzen-Approximation der Diffusionsterme

Durch Einsetzen dieser Ausdrücke in Gleichung (3.2-3) folgt für jedes Kontrollvolumen eine implizite Differenzengleichung der Form

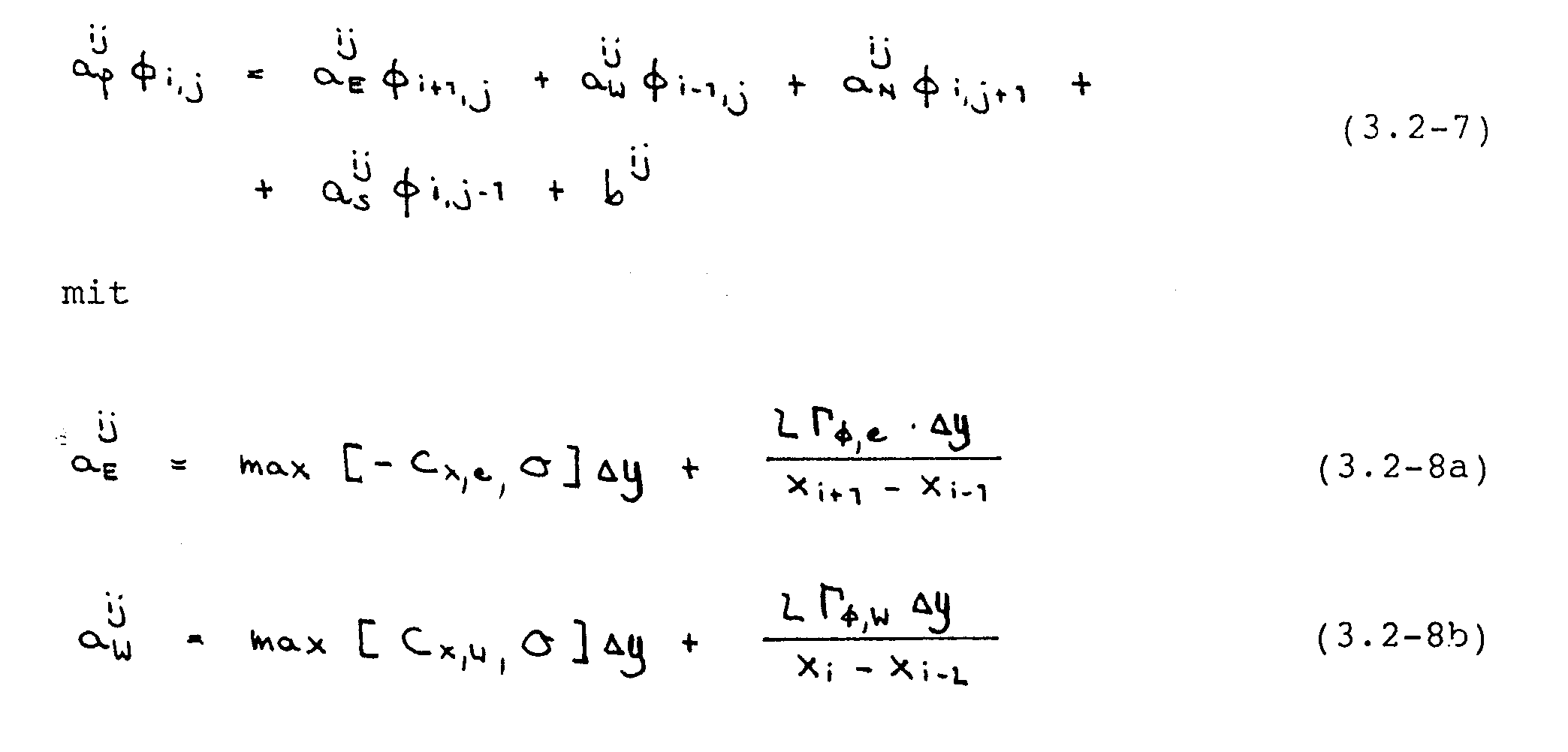
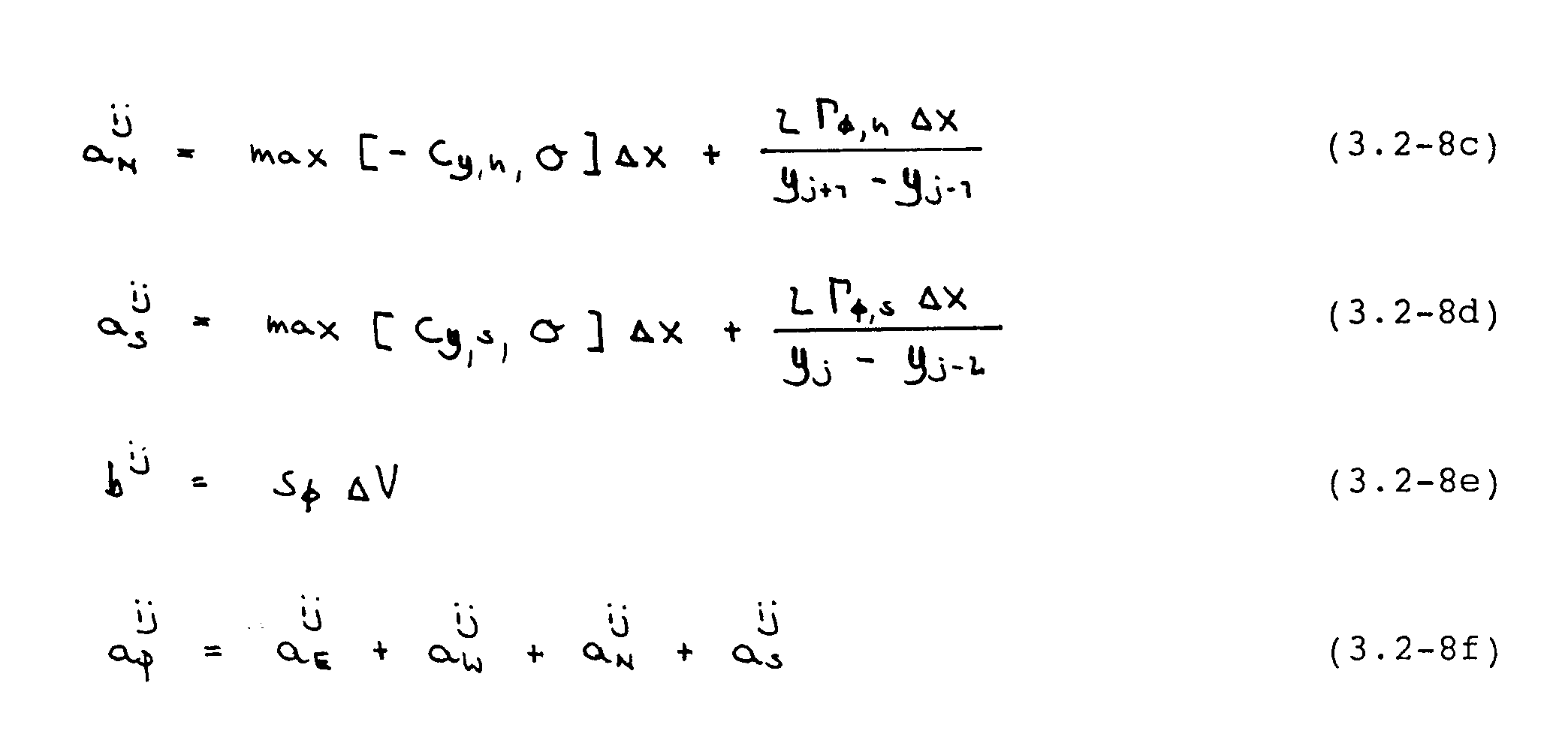
An dieser Stelle sei bemerkt, daß die Koeffizienten in Gleichung (3.2-7) wegen der Verwendung des versetzten Gitters für die U- und V-Gleichung unterschiedlich sind, da z.B. die Massenströme jeweils an anderen Stellen ausgewertet werden müssen.

 

3.3. Druck-Ges chwindigkeitskopplung

Die diskretisierten Impulsgleichungen lauten folgendermaßen :

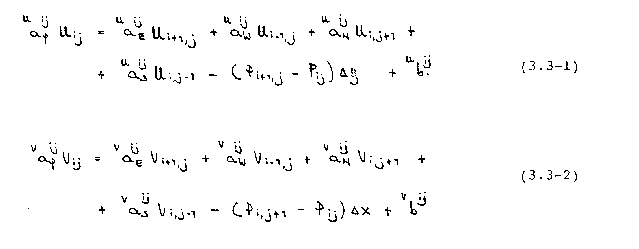
Diese könnten mit einem geeigneten Lösungsalgorithmus nach U und V aufgelöst werden, wenn der Druck P bekannt wäre. Da für den Druck keine eigene Transportgleichung, sondern mit der Kontinuitätsgleichung (2.2-1) nur eine Kompatibilitätsbedingung zwischen den Geschwindigkeiten vorliegt, muß dieser bei den hier betrachteten inkompressiblen Strömungen mit einer speziellen Methode ermittelt werden.

Dazu wird der von Patankar und Spalding (1972) entwickelte SIMPLE-Algorithmus (Semi-Implicit Method for Pressure-Linked Equations) verwendet. Die einzelnen Schritte dieses Verfahrens sind :

1) Schätzung eines Druckfeldes [P*], z.B. [P*] = 0

2) Lösung der diskretisierten Impulsgleichungen (3.3-1) und (3.3-2) mit dem geschätzten Druckfeld; dies ergibt die Geschwindigkeitsfelder [U*I und [V*].

3. Da das geschätzte [P*] i.a. falsch ist, erfüllen die damit berechneten Geschwindigkeitsfelder [U*] und [V*] die Kontinuitätsgleichung nicht.
4. In der unten beschriebenen Weise werden Druck- und Geschwindigkeitskorrekturen [P‘], [U‘], [V‘] abgeleitet, so daß die korrigierten Werte

[U**] = [U*] + [U‘] (3.3-3a)

[V** ] = [V*] + [V‘] (3. 3-3b)

[P**] = [P*] + [P‘] (3. 3-3c)

die Kontinuitätsgleichung erfüllen. Infolge dieser Korrektur werden aber die diskretisierten Impulsgleichungen nun nicht mehr erfüllt.

5) Die Schritte 2) - 4) werden so lange wiederholt, bis die Impuls- und Kontinuitätsgleichuflgen simultan erfüllt sind.

Nachfolgend werden die entsprechenden Beziehungen abgeleitet. Diskretisierung der Kontinuitätsgleichung in einem Druckkontrollvolumen ergibt

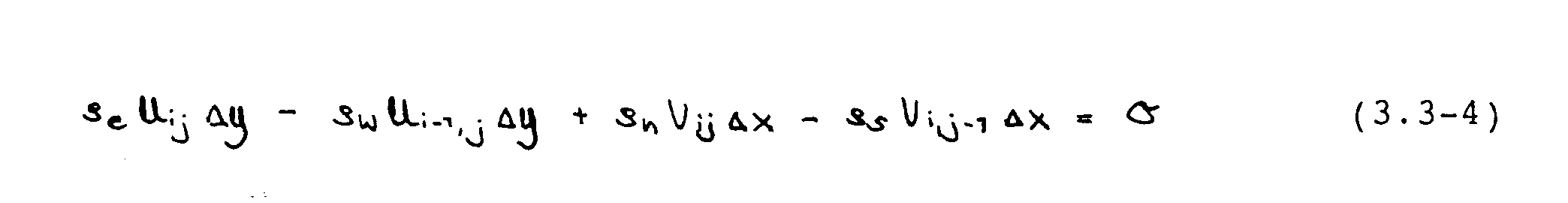
Im versetzten Gitter können die vorkommenden Massenströme ohne Interpolation bestimmt werden, da sie an den Grenzflächen der Druckkontrollvolumina gespeichert sind. Einsetzen der Geschwindigkeitsfelder [U*] und [V*] liefert eine "Massenquelle" S_m, gemäß

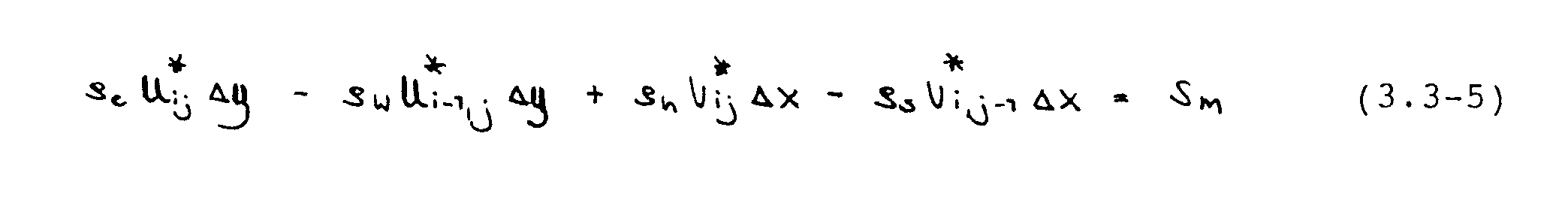
Diese kann zu Null gemacht werden, wenn die vorliegenden Geschwindigkeiten mit Korrekturen U‘ und V‘ versehen werden. Die Definitionsgleichung für diese Korrekturen ist also:

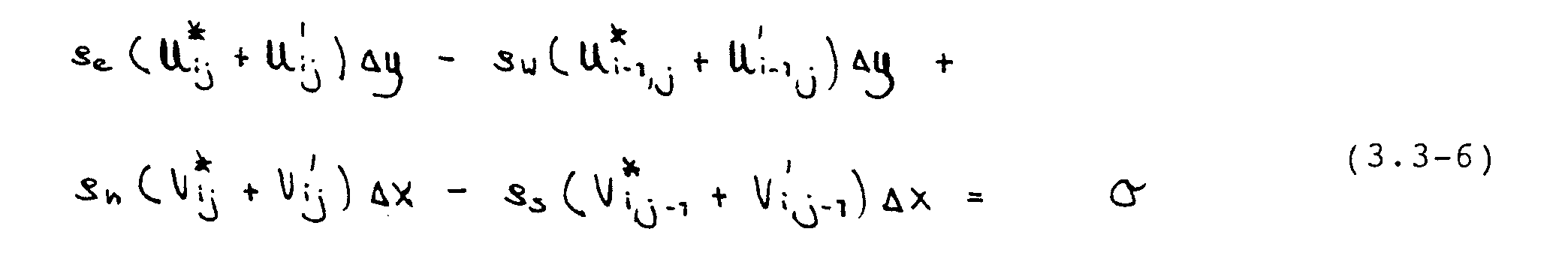
Subtraktion dieser Beziehung von Gleichung (3.3-5) liefert einen Ausdruck für die Geschwindigkeitskorrektulen :

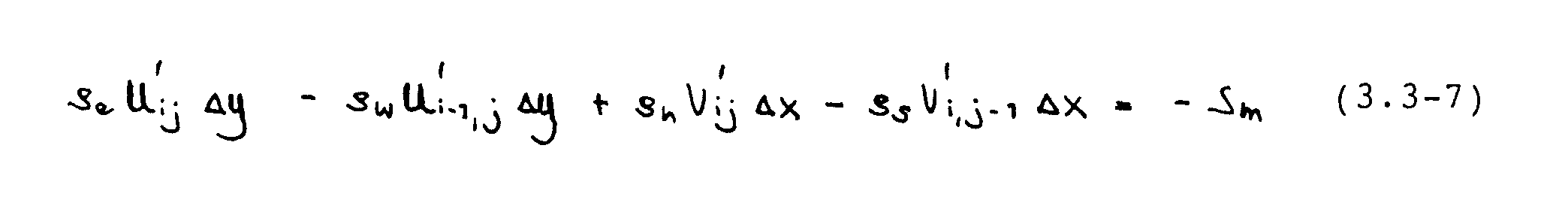
Rein physikalisch können diese Geschwindigkeitskorrekturen nur entstehen, wenn die Drücke um entsprechende Beträge P‘ geändert werden. Ein Zusammenhang zwischen den Druck- und Geschwindigkeitskorrekturen läßt sich aus den diskretisierten Impulsgleichungen ableiten. Durch Abziehen der mit den [U*]- und [P*]- Feldern gebildeten Impulsgleichungen von den exakten Impulsgleichungen (3.3-1) und (3.3-2) folgt eine Gleichung der Form

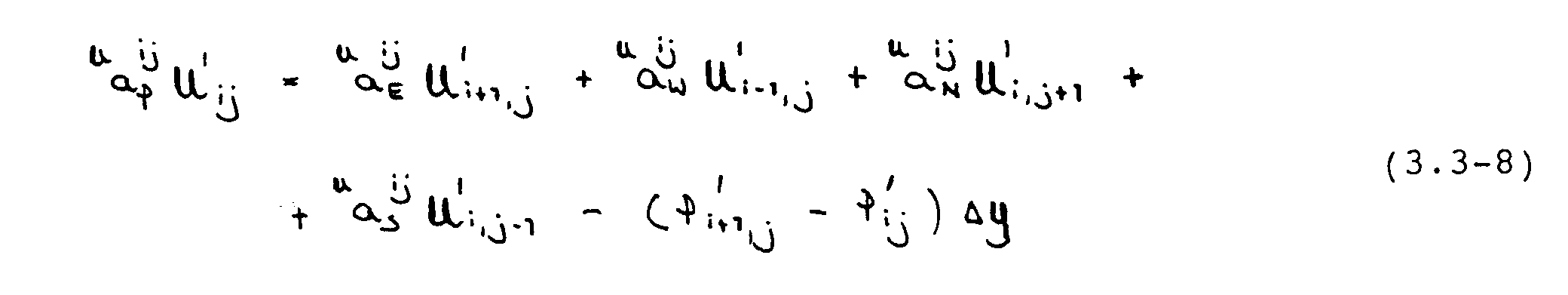
Im SIMPLE-Verfahren wird der implizite Einfluß der Geschwindigkeitskorrekturen an den Nachbargitterpunkten von U_i,j vernachlässigt, was auf

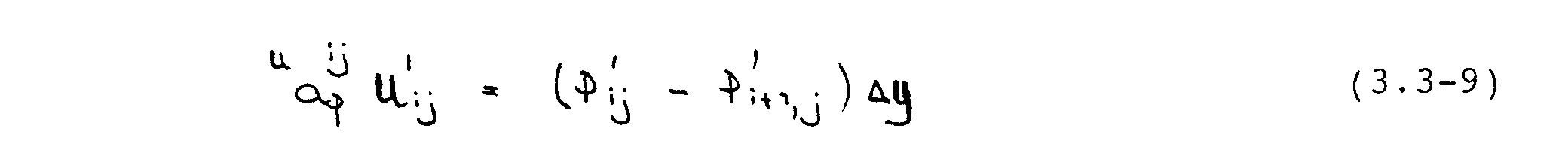
führt: die Gleichung wird semi-implizit. Analoge Ausdrücke können für die restlichen Geschwindigkeitskorrekturen in Gleichung (3.3-7) abgeleitet werden. Substitution dieser Ausdrücke liefert die sog. Druckkorrekturgleichung

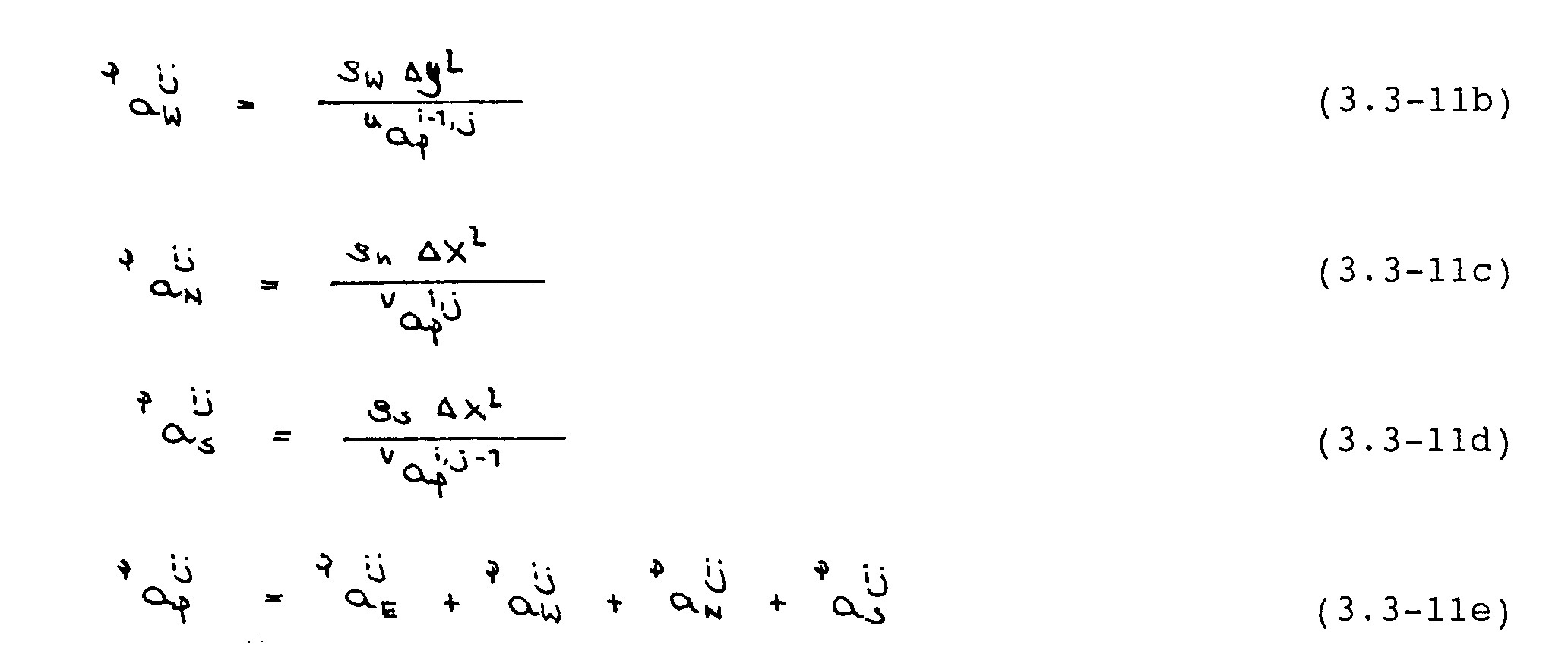
Die Druckkorrekturgleichung besitzt die selbe Form wie die diskretisierten Impulsgleichungen und kann deshalb mit den selben Verfahren gelöst werden. Vorher müßen jedoch entsprechende Randbedingungen spezifiziert werden. Dies wird nachfolgend kurz beschrieben. Details werden von Patankar (1980) angegeben.

In dem hier behandelten Beispiel der Strömung über eine rückwärtsspringende Stufe sind die Normalgeschwindigkeiten entlang aller Ränder bekannt. An den Wänden sind sie gleich Null und an den Ein- und Austrittsebenen werden sie vorgeschrieben. Dies kann zur Formulierung der Randbedingungen für die Druckkorrekturgleichung ausgenutzt werden. Die Geschwindigkeitskorrekturen an den Rändern sind dann identisch Null, was nach Umformung dazu führt, daß die entsprechenden Koeffizienten in der Druckkorrekturgleichung ebenfalls zu Null werden. Dies entspricht physikalisch einer von Neumann-Randbedingung für die Druckkorrektur P‘, wobei deren Gradienten normal zu allen Rändern des Integrationsgebietes zu Null gesetzt werden.

 

3.4. Unterrelaxationsverfahren

Wegen der Annahmen, die zu Gleichung (3.3-9) führten, sind die resultierenden Druckkorrektuzen i.a. etwas zu groß. Dies kann zur Divergenz des SIMPLE-Algorithmus führen, falls keine Unterrelaxation verwendet wird. Im CAST-Programm wird der Druck deshalb nicht mittels Gleichung (3.3-3c) sondern mit

[P**] = [P*] + -±^P [P‘] (3.4-1)

verbessert. -±^P ist der Unterrelaxationsfaktor für den Druck.

Die Geschwindigkeiten U und V werden wie folgt unterrelaxiert. Auf der linken Seite der algebraischen Bestimmungsgleichung (3.2-7) für die allgemeine Variable -¦= (U, V) wird der Wert -¦* vom vorhergehenden Iterationsschritt addiert und subtrahiert :

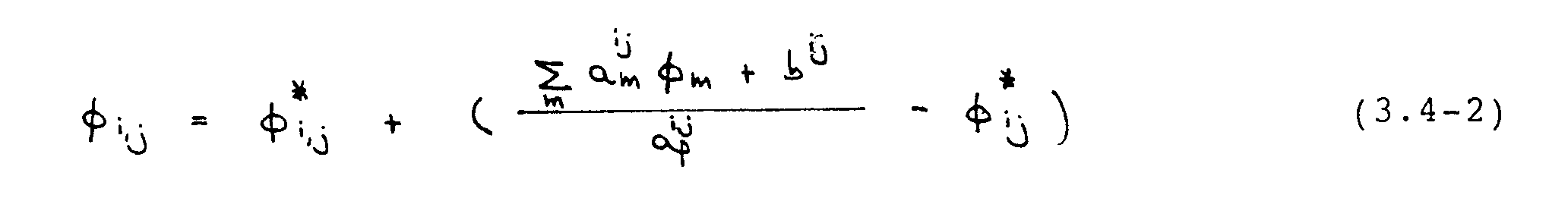
Der Index "m" läuft über die Nachbargitterpunkte E, W, N, S. Der Term in der Klammer stellt die Änderung von -¦ während einer Iteration dar. Dieser wird im Verfahren mit dem Faktor -±^-¦ unterrelaxiert, gemäß :

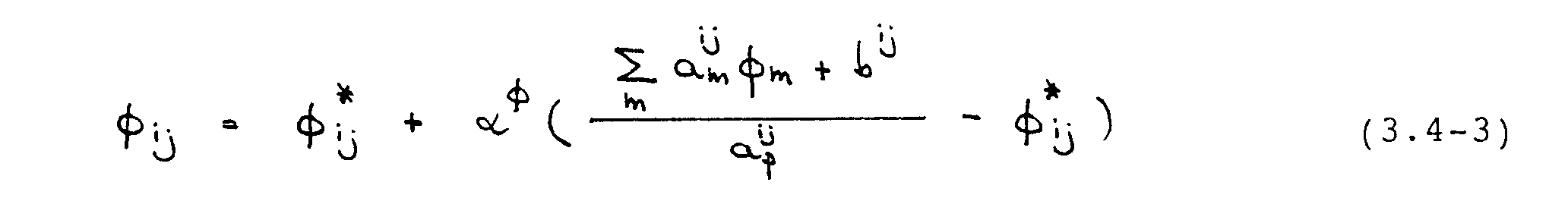
Gute Konvergenz wird bei der Lösung der Navier-Stokes-Gleichungen i.a. erzielt, wenn gilt (Peric et al., 1987)

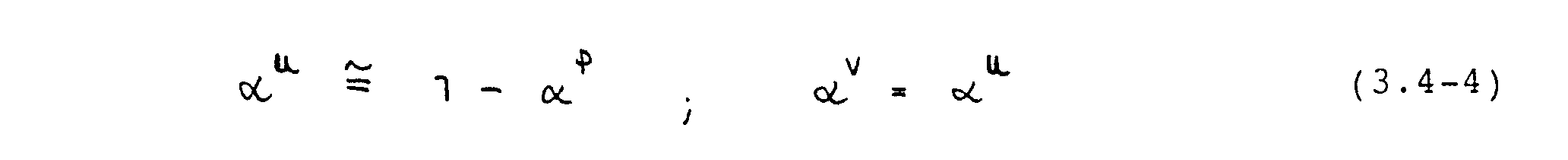
In dieser Arbeit wurden die folgenden Unterrelaxationsfaktoren verwendet

3.5. Lösungsalgorithinen

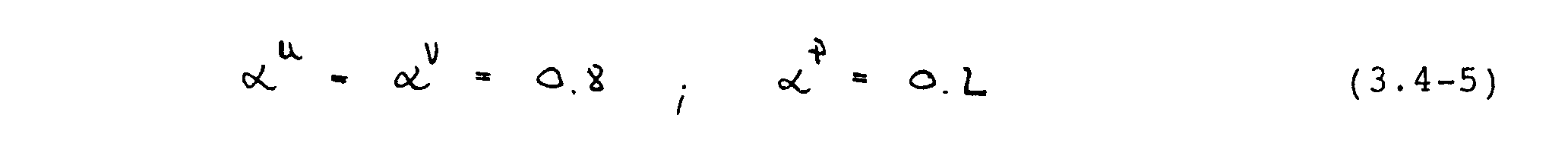
Die Gleichungen (3.3-1), (3.3-2) und (3.3-10) stellen lineare, algebraische Systeme zur Berechnung der [U]-, [V]- und [P‘]-Felder dar. Sie können in Matrixform geschrieben werden. Die Koeffizientenhnatrix [A] besitzt für die geschilderte Diskretisierung fünf von Null verschiedene Elemente pro Zeile und ist positiv definit sowie diagonaldominant. Da direkte Methoden zur Lösung solcher Systeme zu aufwendig sind, werden gewöhnlich iterative Verfahren verwendet. Nachfolgend werden die zwei, in dieser Arbeit eingesetzten Lösungsalgorithmen beschrieben, ein linieniteratives Verfahren in Abschnitt 3.5.1 und die bekannte Gauß-Seidel-Methode in Abschnitt 3.5.2.

 

 

3.5.1. Linieniterative Methode

Die Koeffizientenmatrix [A] kann, wie in Abb. 3.5a gezeigt, in Form eines Block-Tridiagonalsystems geschrieben werden. Die Untermatrizen [A_P] sind tridiagonal. [A_S] und (A_N] sind Diagoalmatrizen. Jeder der Vektoren [-¦_j] entspricht einer Zeile mit y = const. im numerischen Gitter.

Die in Abb. 3.5b dargestellte Umformung des Gleichungssystemes bildet die Basis für den linieniterativen Iterationsprozeß. Auf der linken Seite treten nur mehr Tridiagonalmatrizen auf die mit dem Thomas-Algorithmus effizient gelöst werden können. Der Iterationsprozess läuft wie folgt ab:

Die Lösung wird auf der zweiten Kontrollvolumenzeile begonnen, d.h. mit dem Vektor [-¦2]. Dazu wird das Produkt [A_N][-¦3] auf der rechten Seite des Systems in Abb. 3.5 ben-Ætigt. Da [-¦3] noch nicht vorliegt, werden daf-Ìr anfänglich Schätzwerte verwendet. Nachdem der Vektor [-¦2] mit Hilfe des Thomas-Algorithmus (d.h. mit einer direkten Methode) berechnet wurde, wird zum übernächsten Zeilenvektor [-¦4] bzw. allgemein [-¦j] vorw-´rtsge schritten.

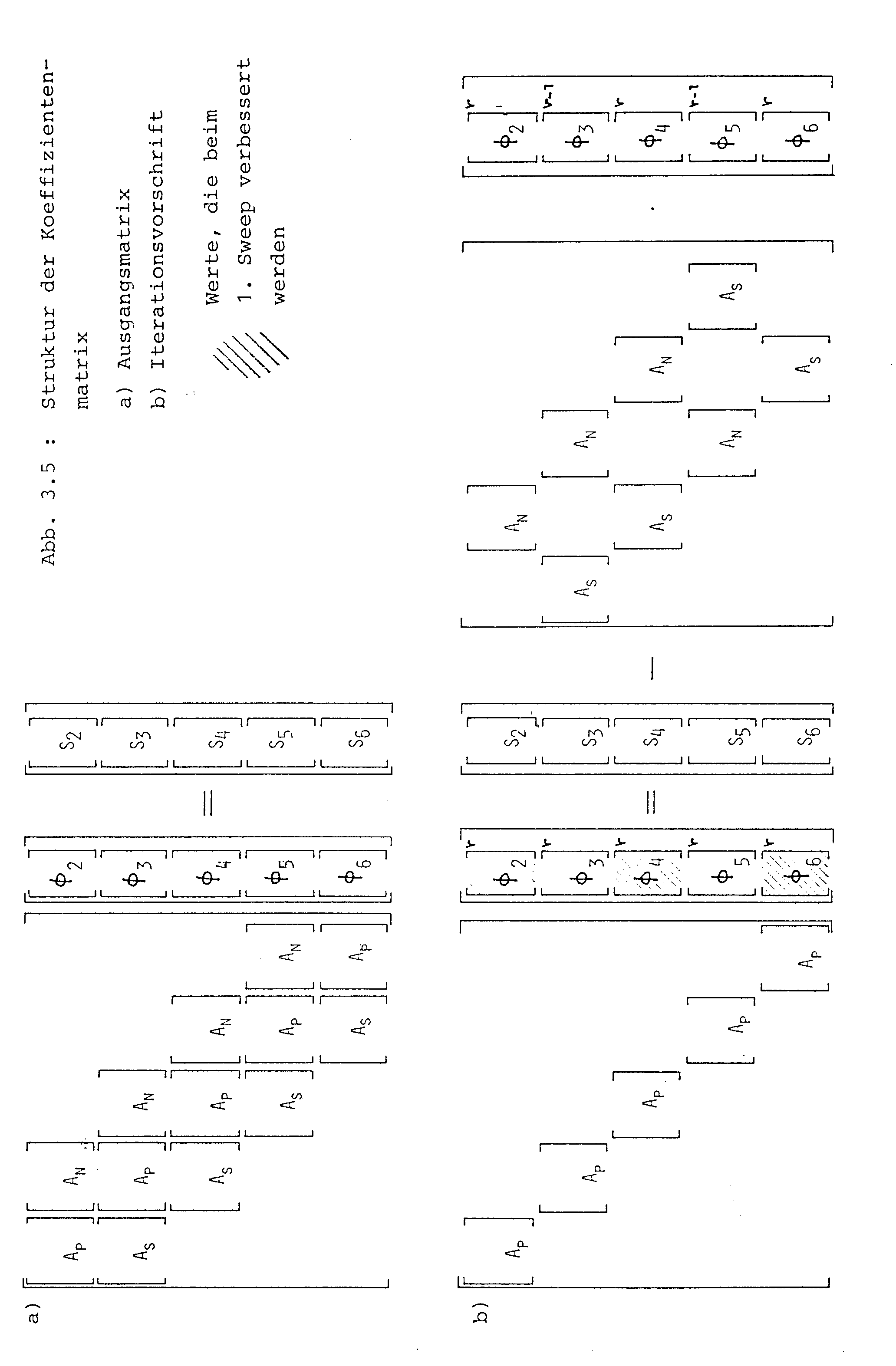
Hier müssen die Produkte [As][-¦_j-1] und [A_N][-¦_j+1] gebildet werden. Dazu werden wieder die Anfangsschätzwerte benutzt. In dieser Weise wird das gesamte Lösungsgebiet abgearbeitet, wobei auf der rechten Seite des Gleichungssystems in Abb. 3.5b jeweils nur Schätzwerte bzw. Werte von der vorausgegangenen Iteration stehen. Beim zweiten Durchgang durch das Lösungsgebiet wird die Prozedur mit der dritten Zeile begonnen. Die dazu benötigten Produkte [A_N][-¦4] und [A_S][-¦₂] werden nun mit den im ersten Sweep errechneten Werten gebildet. Danach wird zur übernächsten Zeile weitergegangen, usw. bis das Lösungsgebiet ein zweites Mal überstrichen ist. Dies liefert einen vollständigen neuen Lösungsvektor [-¦].

Die Gesamtprozedur wird so lange wiederholt, bis entweder das Konvergenzkriterium oder die vorgegebene Maximalanzahl von inneren Iterationen (Sweeps) erreicht ist. Innerhalb des SIMPLE-Algorithmus ist es nicht notwendig, die einzelnen Gleichungen jeweils bis zur vollständigen Konvergenz zu lösen, da nach der Lösung die errechneten Funktionswerte korrigiert und in der Folge auch die Matrixkoeffizienten neu bestimmt werden. Es muß jedoch sichergestellt sein, daß die U- und V-Gleichungen und speziell die Druckkorrekturgleichung für sich jeweils konvergieren, da sonst der gesamte SIMPLE-Algorithmus nach wenigen Iterationen divergiert.

In dieser Arbeit wurde die Anzahl der inneren Iterationen, d.h. der Durchläufe durch die Koeffizientenmatrizen, fest vorgeschrieben und zwar 5 Sweeps für die U- und V-Gleichungen und 40 für die Druckkorrekturgleichung. Die U- und V-Gleichungen sind einfacher zu lösen, da einerseits jeweils die vom vorhergehenden Iterationsschritt im Speicher befindlichen Felder als Anfangsschätzwerte verwendet werden können und andererseits an drei Rändern Diriclet-Randbedingungen vorliegen. Für die Druckkorrekturgleichung gilt dies nicht; die Lösung wird hier in Ermangelung besserer Werte mit der Anfangsschätzung [P‘] = 0 gestartet. Zudem sind bei der Druckkorrekturgleichung an allen Rändern von Neumann-Randbedingungen vorgeschrieben, was die Konvergenz negativ beeinflußt.

 

 

3.5.2. Gauß-Seidel-Methode

Das Gauß-Seidel-Verfahren ist punktiterativ; die Iterationsvorschrift lautet

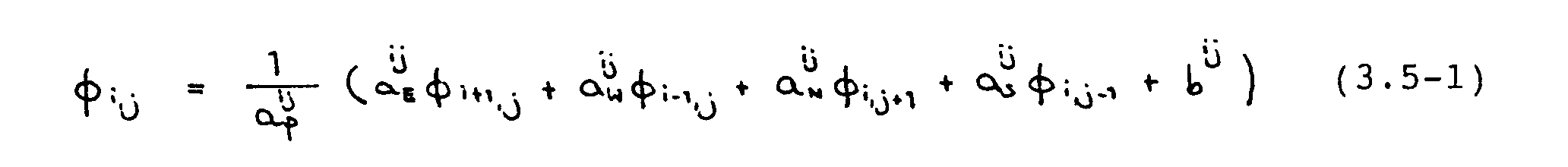
In dieser Arbeit wurde die sog. Red-Black-Variante benutzt. Das Lösungsgebiet wird dabei, wie auch beim linieniterativen Verfahren, zweimal durchlaufen. Im ersten Durchgang werden, ausgehend von der linken unteren Ecke des Integrationsgebietes, punktweise neue -¦-Werte berechnet, wobei in Form eines Schachbrettmusters jeweils ein Punkt -Ìbersprungen wird ("rote" Punkte). Auf der rechten Seite von Gleichung (3.5-1) stehen beim ersten Sweep dann nur Schätzwerte bzw. bei den folgenden Sweeps Werte aus der vorhergehenden Iteration. Im zweiten Durchgang werden die "schwarzen" Punkte berechnet. Dazu werden auf der rechten Seite von Gleichung (3.5-1) die im ersten Durchgang errechneten -¦_ij‘s eingesetzt.

Der gesamte Ablauf wird, wie im vorigen Abschnitt erläutert, bis zum Erreichen des Konvergenzkriteriums bzw. der spezifizierten Maximalanzahl von Iterationen wiederholt.

 

3.5.3. Bewertung der Lösungsalgorithimen

Die Lösungsalgorithmen sind ein wichtiger Programmteil, da in ihnen der Großteil der Gesamtrechenzeit verbraucht wird. Deshalb ist es notwendig, möglichst effiziente Verfahren einzusetzen. Hier ist jedoch bei Parallelrechnern ein Kompromiß einzugehen. Das in Abschnitt 3.5.2 vorgestellte Gauß-Seidel-Verfahren läßt sich z.B. mit einer hohen Effizienz parallelisieren. Das Verfahren an sich konvergiert aber mit steigender Gitterpunktzahl (speziell bei Problemen mit von NeumannRandbedingungen, wie z.B. bei der Druckkorrekturgleichung) äußerst langsam. Der Zeitgewinn durch den parallelen Ablauf des Verfahrens kann im Extremfall durch dessen schlechte Effizienz wieder ausgeglichen werden. Dies war z.B. der Grund, warum die Gauß-Seidel-Methode nach einigen anfänglichen Berechnungen in dieser Arbeit nicht weiter verwendet wurde.

Die serielle Effizienz des linieniterativen Verfahrens erhöht sich i.a., falls die direkte Lösung der Tridiagonalsysteme nicht nur entlang Linien y = const., sondern abwechselnd entlang Linien y = const. und x = const. durchgeführt wird. Mit der in dieser Arbeit verwendeten DIRMU-Konfiguration nimmt dadurch jedoch die Parallelisierbarkeit ab. Deshalb wurde in dieser Arbeit auf diese Maßnahme verzichtet.

In der Ursprungsversion des Programmes CAST (Peric und Scheuerer, 1987) ist zur Lösung der Druckkorrekturgleichung das Verfahren von Stone (1968) eingebaut; dieses basiert auf einer unvollständigen LU-Zerlegung. Die serielle Effizienz dieses Verfahrens bei der Lösung der Druckkorrekturgleichung ist wesentlich höher, als die der beiden erst genannten Verfahren (Peric, 1987 und Barcus, 1987). Das Verfahren von Stone (1968) läßt sich jedoch nur ungenügend parallelisieren. In zukünftigen Arbeiten sollte jedoch genau abgewogen werden, ob eine solche Methode - trotz geringerer Parallelisierbarkeit - nicht eine höhere Gesamteffizienz bietet.

 

3.6. Konvergenzkriterium

Das Konvergenzkriterium ist wie folgt: Nachdem die Koeffizienten in Gleichung (3.2-7) berechnet sind, werden die Residuen für die U- und V-Kontrollvolumina jeweils nach der Beziehung

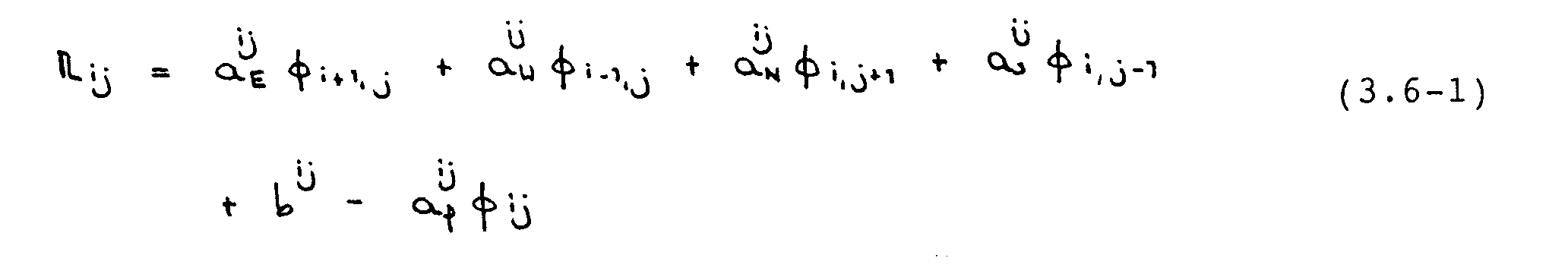
ermittelt. Im Falle der Kontinuitätsgleichung ist die Massenquelle Sm das Residuum. Für alle Variablen wird die Summe der absoluten Residuen gebildet und auf eine geeignete Größe F_-¦ bezogen. Für F_-¦ wurden die einströmenden Massen- bzw. Impuls-flüsse verwendet. Es wird dann gefordert, daß diese normierten Größen kleiner als ein vorgegebenes Konvergenzkriterium -µ sind, d.h. daß gilt

In dieser Arbeit wurde -µ= 0.005 gew-´hlt.

 

4. DIRMU-Multiprozessor

 

4.1. Hardware

Der DIRMU-Multiprozessor (Händler et al., 1985) wurde an der Universität Erlangen-Nürnberg zum Testen von Multiprozessor-Konfigurationen und paralleler Programmierung entwickelt. Die Grundidee von DIRMU ist der Aufbau eines weiten Spektrums spezieller Multiprozessor-Konfigurationen mit einem universellen Bausteintyp. Ein solcher Baustein ist in Abb. 4.1 dargestellt. Er besteht aus einem Prozessor-Modul (P-Modul) und einem Multiportspeicher-Modul (M-Modul). Beide Module besitzen jeweils acht Anschlüße (Ports). Die P-Ports 1 - 7 können durch Kabel mit den M-Ports anderer DIRMU-Bausteine verbunden werden. Die M-Module haben Anschluß an mehrere Prozessoren; von diesen kann direkt auf die Daten im Multiportspeicher zugegriffen werden.

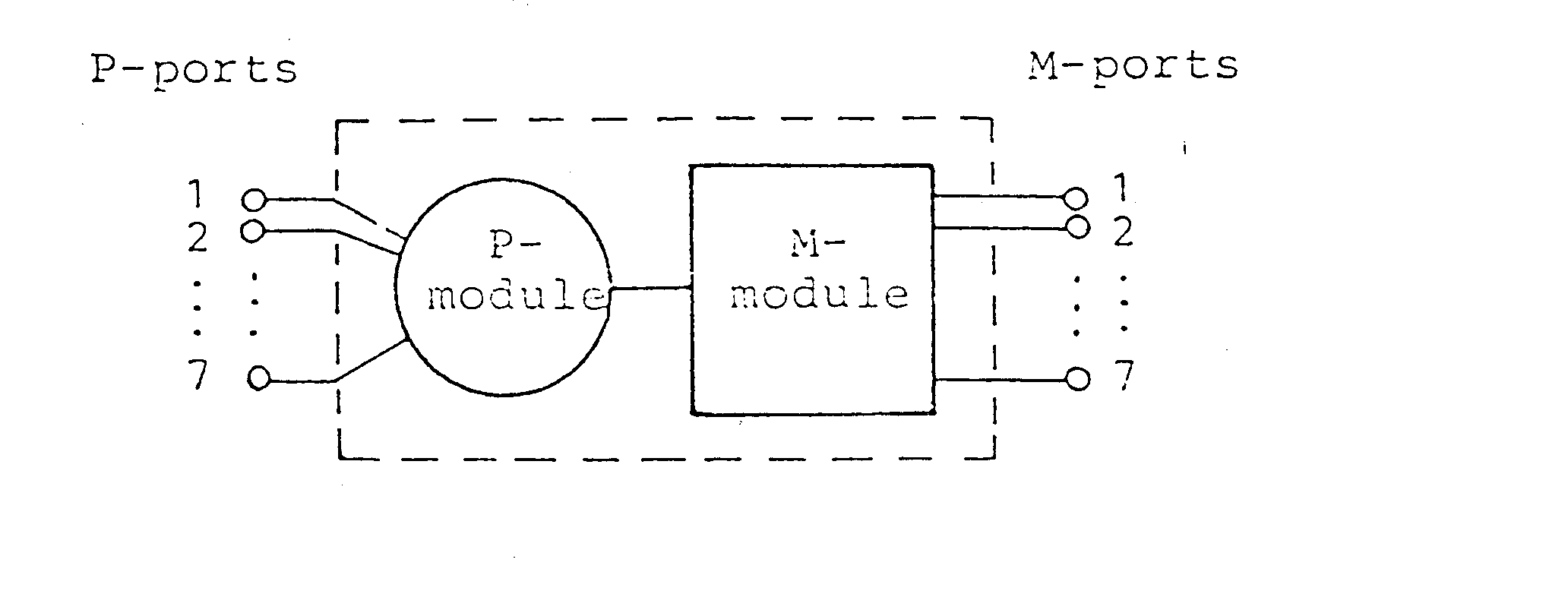
Abb. 4.1 : DIRMU-Baustein

Mit diesen Elementen können verschiedene Rechnerkonfigurationen aufgebaut werden. Abb. 4.2 zeigt einige Beispiele. Im Prinzip können beliebig viele Prozessoren kombiniert werden. Es werden jedoch nur immer maximal sieben Prozessoren direkt miteinander verbunden, d.h. es handelt sich um eine Struktur mit begrenzter Nachbarschaft.

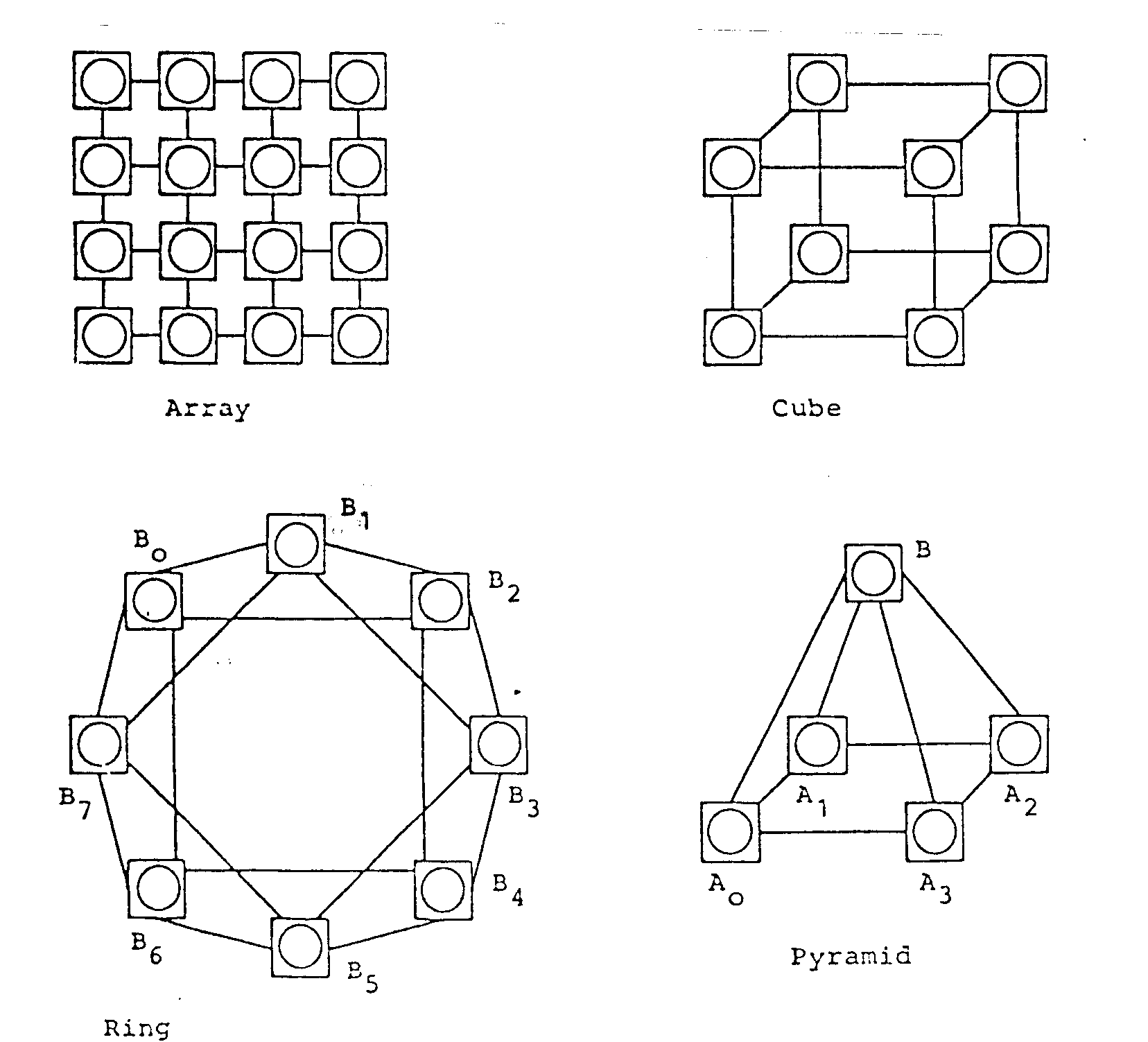
Abb. 4.2 Beispiele von DIRMU-Konfigurationen

In Abb. 4.3 ist ein Einzelbaustein in größerem Detail dargestellt. Im P-Modul arbeiten der Mikroprozessor 8086 und der arithmetische Coprozessor 8087 der Firma INTEL. Uber einen internen Bus haben die Prozessoren Zugriff auf 16 kByte privaten Nur-Lese-Speicher (RAM) und 320 kByte privaten Speicher (ROM) sowie auf Schnittstellen für Terminal, Drucker, Massenspeicher usw. Der M-Modul enthält 64 kByte Speicher und 8 M-Ports. Über P-Port 0 und M-Port 0 kann jeder Prozessor auf seinen eigenen M-Modul zugreifen.

Der gegenseitige Speicherzugriff wird an Hand des Beispieles der Abb. 4.4 erklärt. Die Datenzone A wird vom Prozessor P₀ ab der Adresse 1:6000h (Segment: 1, Offset: 6000h) gesehen. Auf die gleiche Datenzone kann von Prozessor P₂ ab der Adresse 2:6000h und von P₁ ab der Adresse 7:6000h zugegriffen werden. Von einem Prozessor angeforderte Adressen werden von der P-Port-Steuerung decodiert. Die Segmentnummer entspricht jeweils der um Eins vermehrten P-Port-Nummer. Der 0ffset bleibt unverändert.

 

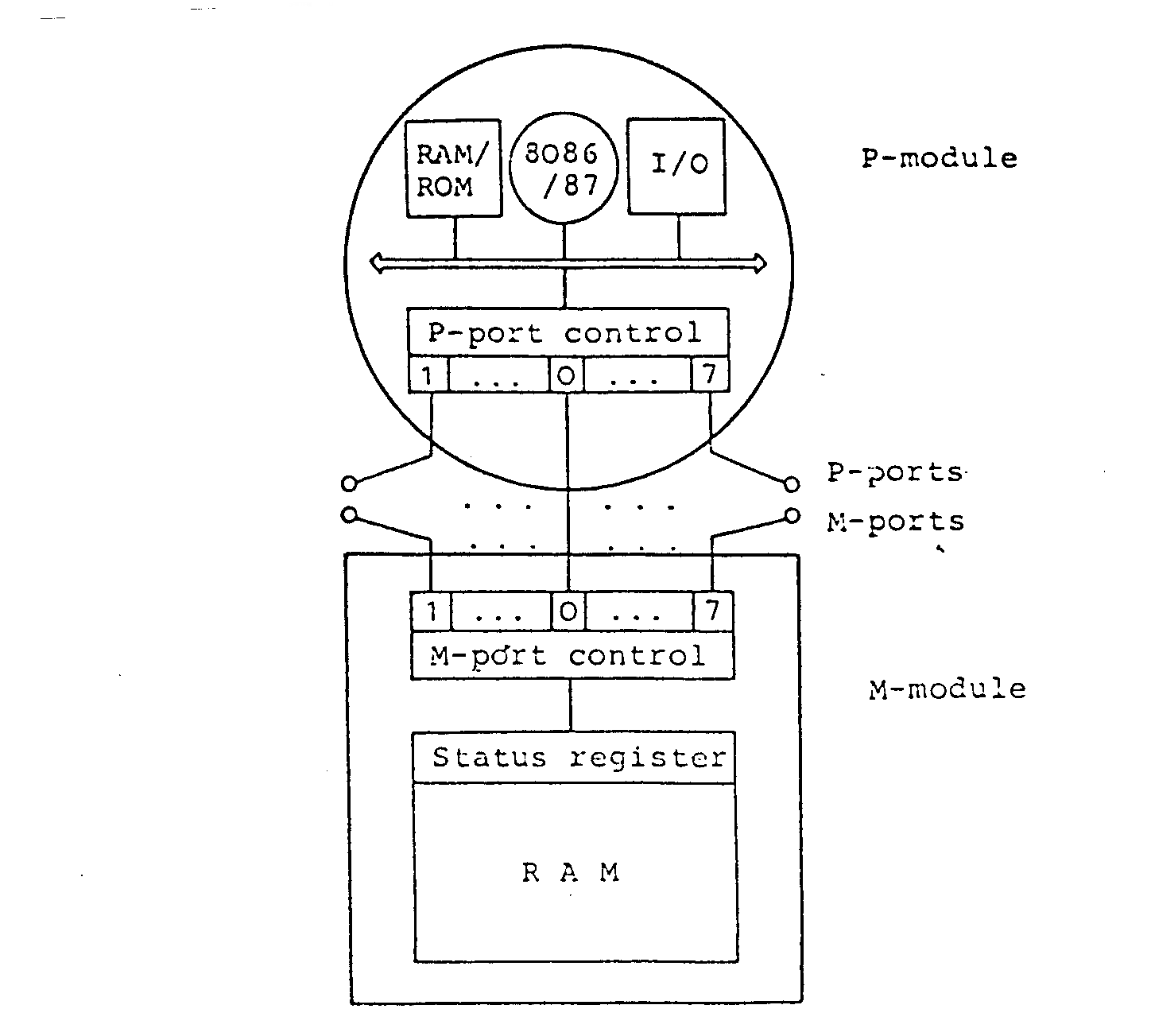
Abb. 4.3 : Struktur eines DIRMU-Einzelbausteines

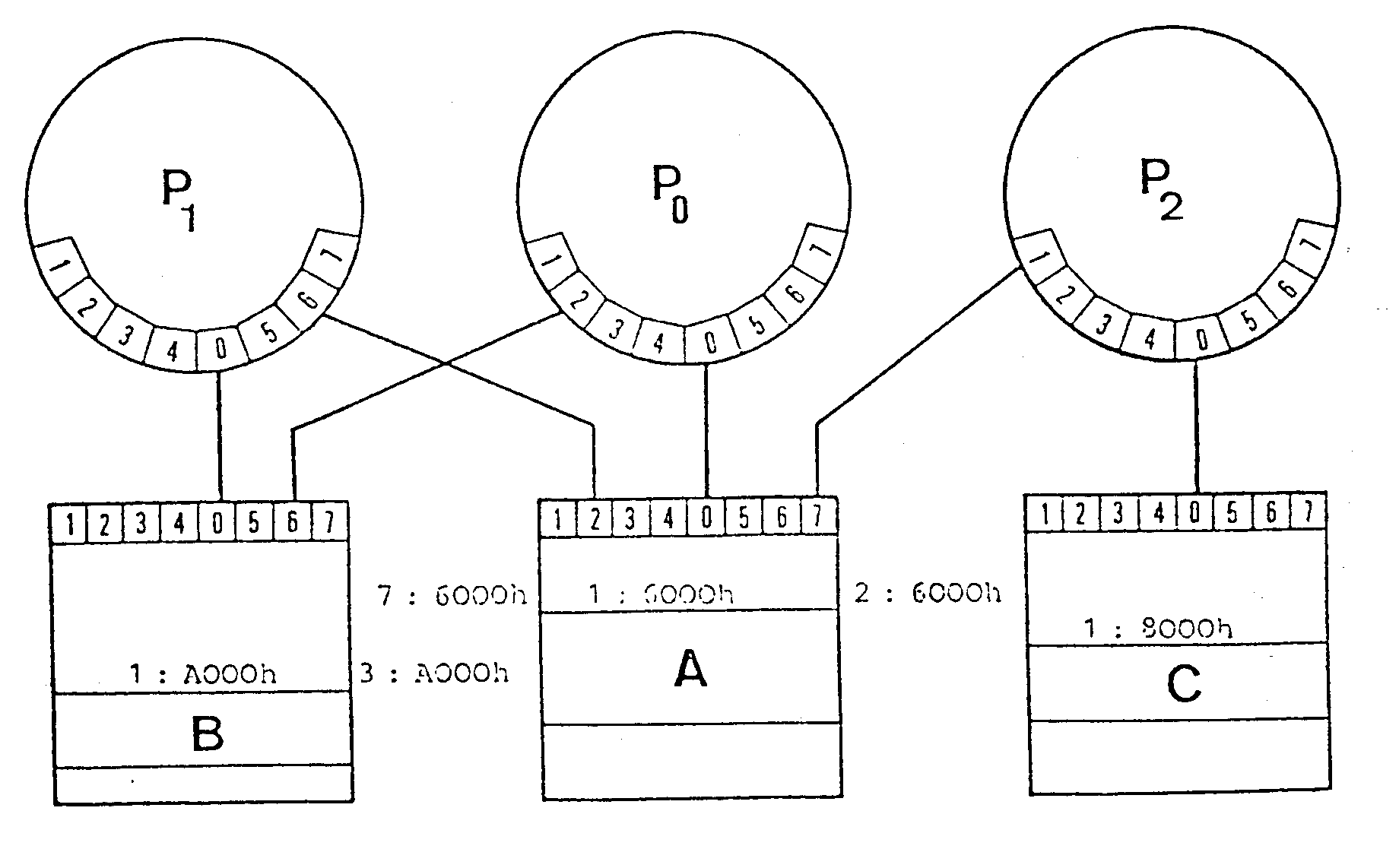
Abb. 4.4 : Adressierung von Daten in den M-Modulen

Die Datenwortlänge ist 16 Bit. Die Zugriffszeit beträgt 800 ns für den privaten Speicher und - ohne Zugriffskonflikt - 1200 ns für den Multiportspeicher. Die größere Zugriffszeit für den Multiportspeicher wird durch den langsameren RAM-Speicher und den Kontrollzeiten am P- und M-Port verursacht. Es ist wichtig, daß alle an einem Prozessor angeschlossenen Multiportspeicher die selbe Zugriffszeit haben.

Jeder Prozessor besitzt seine eigene Uhr. Greift mehr als ein Prozessor auf den gleichen Multiportspeicher zu, entsteht ein Zugriffskonflikt, der von der M-Port-Steuerung behoben wird. Ein Prozessor wartet, bis er die Daten bekommt. Es gilt die Regel, daß ein Prozessor nicht zweimal nacheinander auf den selben Speicher zugreifen kann, wenn ein anderer Prozessor wartet. Messungen haben gezeigt (Maehle et al., 1985), daß die längeren Zugriffszeiten des M-Moduls und Wartezeiten infolge von Zugriffskonflikten die Laufzeit von Anwenderprogrammen nur geringfügig verlangsamen, da jeweils nur die verteilten Daten in den M-Modulen gespeichert sind. Die meisten Speicherzugriffe betreffen jedoch i.a. den Programmcode und die Daten im Privat-speicher, bei denen keine Zugriffskonflikte entstehen können.

Ein Prozessor kann den Multiportspeicher für mehr als einen Speicherzyklus belegen. Dies ist notwendig für Synchronisierungsvorgänge (Read-Modify-Write) und zur Erhaltung der Konsistenz von Daten, die breiter als ein Wort sind (REALVariable). Die Kommunikation zwischen Prozessoren erfolgt für gemeinsame Daten. Zwei Prozessoren, die das gleiche M-Modul teilen, können sich durch Setzen der Bits in zwei Registern gegenseitig Interrupts senden. Diese Mechanismen werden für die ebenfalls bereitgestellte Möglichkeit des Botschaftsverkehrs genutzt.

Ein weiteres Status-Register in den M-Modulen dient zur Fehlerdiagnose. Bei eigenen Fehlern bzw. Fehlern in Nachbarbausteinen (z.B. Probleme bei der Stromversorgung, illegale HALT-Anweisungen usw.) wird ein entsprechendes Bit in diesen Status-Registern gesetzt und ein Interrupt zu allen Nachbarn gesandt. Die Fehlerdiagnose ist zum Aufbau fehlertoleranter Systeme nötig.

Jeder DIRMU-Baustein besitzt seine eigene Stromversorgung und befindet sich in einem 3/4 19"-Gehäuse, s. Abb. 4.5. Die P- und M-Modul-Verbindungen sowie die Last auf den Forts sind durch zwei LED‘S auf der Vorderseite optisch kontrollierbar.

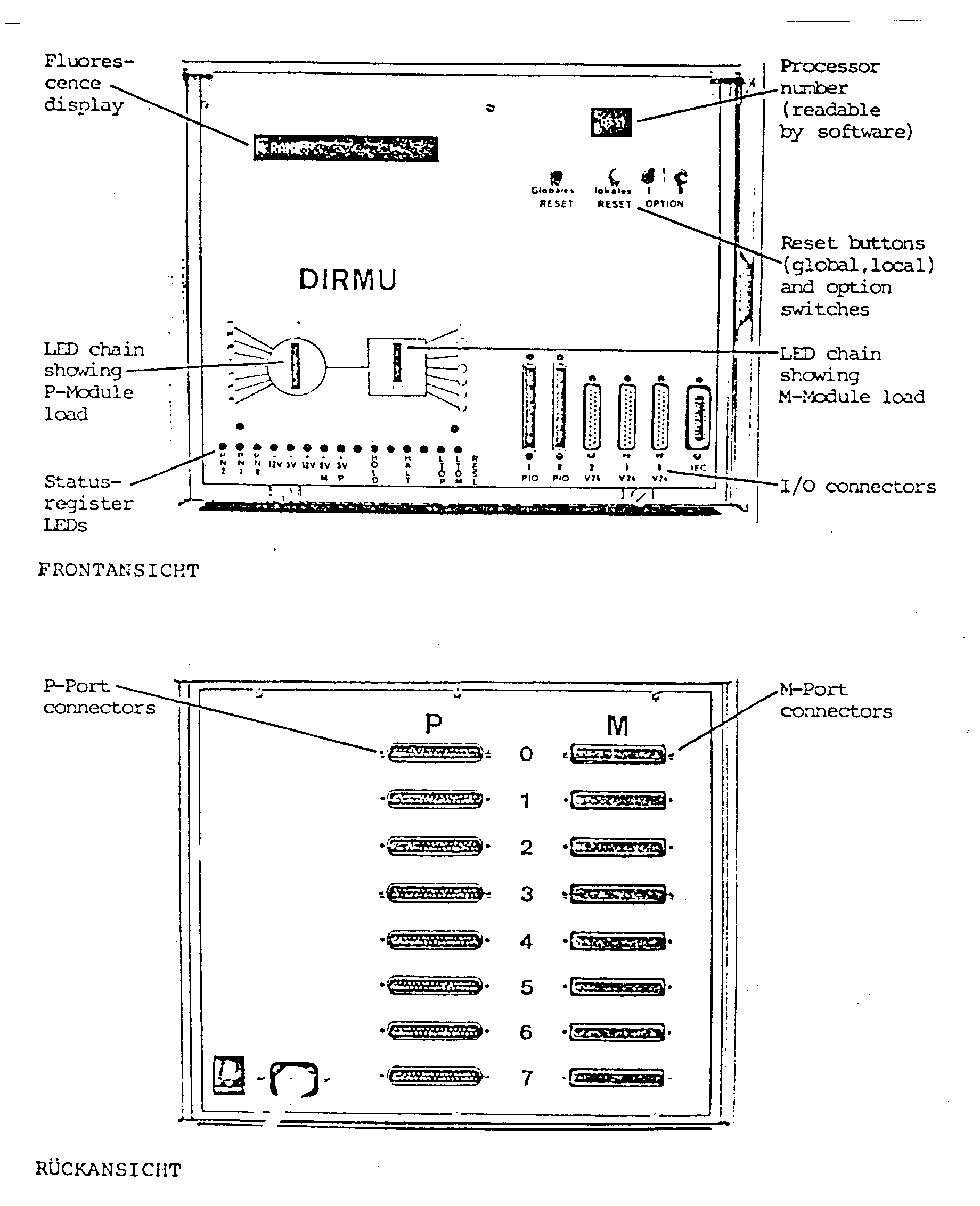
Abb. 4.5 Vorder- und Rückansicht eines DIRMU-Bausteines

 

 

4.2 Betriebssystem und Programmiersprache

In diesem Abschnitt wird das auf DIRMU laufende Betriebssystem DIRMOS (Diagnosis Integrated Reconfiguring Multiprocessor Operating System) beschrieben. Es basiert auf dem Concurrent CP/M-Betriebssystem.

Die Entwicklung paralleler Anwendungsprogramme auf DIRMU folgt dem Master/Slave-Prinzip. Jeder DIRMU-Baustein, der eine Festplatte und ein Terminal enthält (Master), kann in einem Mono-prozessor-Modus als Entwicklungseinheit benutzt werden. In parallelen Anwendungen kontrolliert der Master den Dialog mit dem Benutzer; das Laden eines Mehrprozessorprogrammes erfolgt von seiner Platte. Die weiteren mitarbeitenden Prozessoren sind Slaves. Verschiedene Benutzer können die Maschine so teilen, daß für jeden Master jeweils nur ein Slave reserviert wird (space sharing).

In DIRMOS ist ein Konfigurierungsprogramm zur Erzeugung verschiedener Multiprozessoranordnungen sowie ein Diagnoseprogramm integriert. Während Leerlauf zeiten stellt das Diagnose-programm fest, ob Prozessoren der Gesamtkonfiguration ausgefallen sind. Die Speicherverbindungen werden dabei mit überprüft. Die vom Benutzer gewählte Konfiguration (application configuration), z.B. ein Ring, wird von DIRMOS (configuration finder) auf die intakten Prozessoren abgebildet. DIRMOS liefert die Nummern der logischen Nachbarports für jeden Prozessor sowie seine Lage in der gewählten Anwendungskonfiguration. Zusätzlich enthält DIRMOS einen parallelen Lader, der das Anwendungsprogramm in den Privatspeicher jedes mitarbeitenden Prozessors eingibt.

Im folgenden werden diese Punkte in größerem Detail erläutert. DIRMOS besteht aus drei Hauptteilen

- COMINT

- FINDER

- MANAGER

COMINT stellt den residenten Teil des Betriebssystems dar und wird beim Kaltstart in die Privatspeicher aller Module geladen. Durch ein Steuerzeichen kann ein Prozessor als Master bestimmt werden. Vor dem Starten eines Anwendungsprogrammes muß vom Benutzer eine Konfigurationen gewählt werden. Vom System wird er dabei durch den FINDER unterstützt, der zuvor in den Master geladen wird. Er sucht die größtmögliche Konfiguration dieser Art auf dem Multiprozessorsystem und liefert die Anzahl der maximal zur Verfügung stehenden Prozessoren zurück. Der Benutzer kann innerhalb dieser eine beliebige Prozessorenzahl auswählen. Die entsprechende Anzahl wird daraufhin, vom Master ausgehend, als Slaves zugeordnet und das Anwendungsprogramm über einen Ladebaum gepipelined in alle Prozessoren geladen, s. Abb. 4.6.

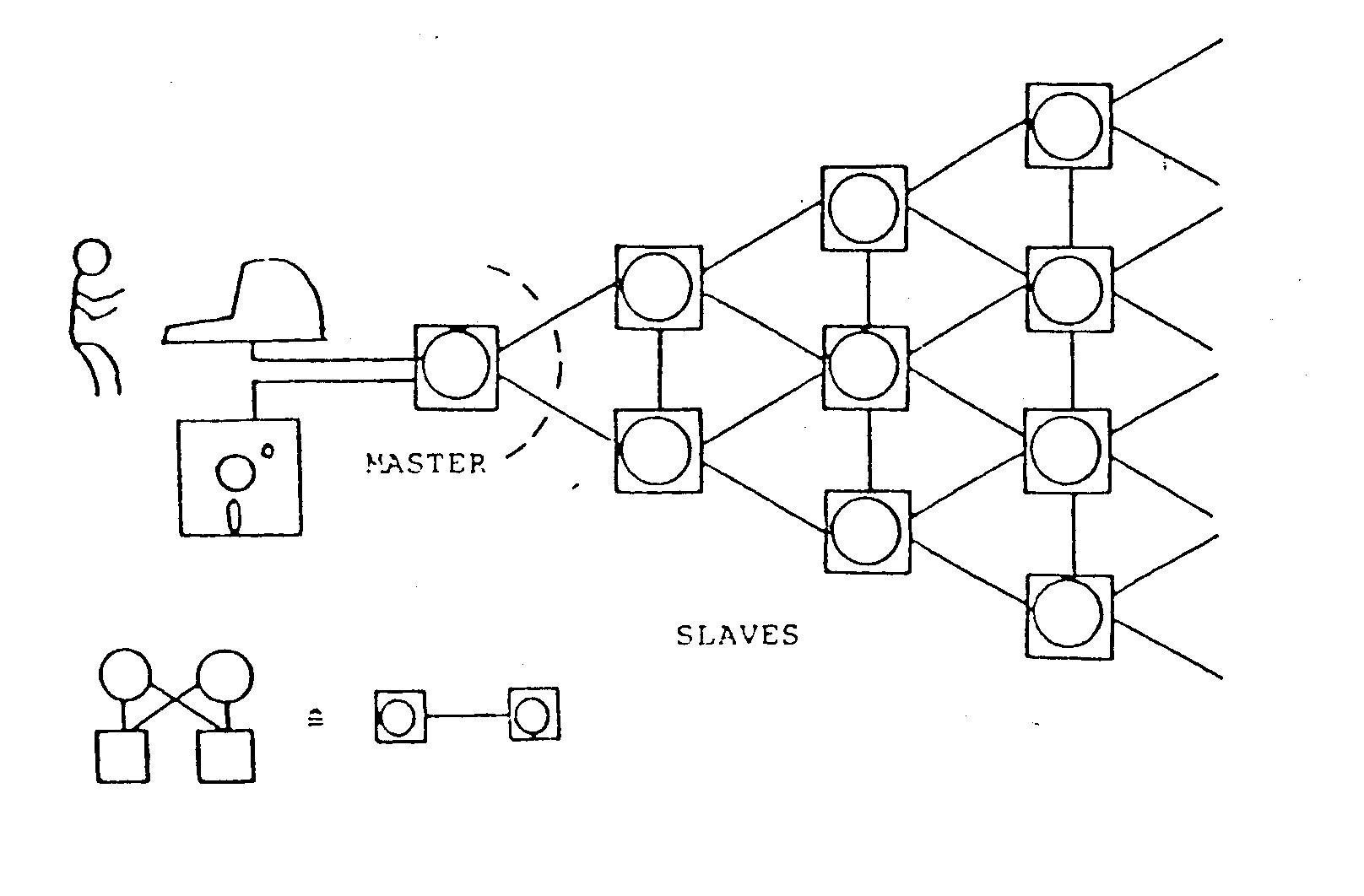
Abb. 4.6 Ladebaum

Der MANAGER ist ein Library-Modul, der mit dem Anwendungsprogramm gelinkt ist. Er berechnet die logische Position des jeweiligen Prozessors in der Anwenderkonfiguration und die Zahl und Nummern der angeschlossenen logischen Nachbarn. Die dafür notwendigen Informationen bezieht er aus den Berechnungen des FINDER. Nach der Initialisierung des MANAGER kennt das Anwenderprogramm die Nummern seiner logischen Nachbarn und kann durch Aufruf des LOCATORS verteilte Datenstrukturen schaffen. Der LOCATOR ist ein Library-Modul, der die entsprechenden Adressen berechnet.

Das Betriebssystem DIRMOS auf DIRMU-25 unterstützt drei Hauptkonfigurationstypen:

• Ringe,
• Felder und
• n-dimensionale Würfel.

Wird eine andere Anwendungskonfiguration gewählt (s. Abb. 4.2), so steht ein Spezialkonfigurator zur Verfügung, dem der Benutzer die gewünschte Rechnertopologie mitteilt.

Als Progranmisprache auf DIRMU wird MODULA-2 (Wirth, 1985) verwendet, das an PASCAL angelehnt ist.

 

5. Parallelisierung des Lösungsverfahrens

In diesem Kapitel wird die Parallelisierung des in Kapitel 3 beschriebenen Lösungsverfahrens diskutiert. Die Gliederung ist wie folgt: im nächsten Abschnitt wird die verwendete Rechner-konfiguration beschrieben; die Aufteilung der Variablen des Anwenderprogrammes und der Ablauf des parallelisierten Verfahrens werden in den Abschnitten 5.2 und 5.3 erläutert. Die für die Parallelisierung nötigen Synchronisierungen werden in Abschnitt 5.4 behandelt.

 

5.1. Rechnerkonfiquration

Der erste Schritt bei der Parallelisierung eines Lösungsverfahrens ist die Auswahl einer geeigneten Rechnerkonfiguration. Für das hier behandelte zweidimensionale Problem mit rechteckigem Integrationsgebiet bietet sich eine

• Feld- oder eine
• Ringstruktur

an (vgl. Abb. 4.2). Wegen der geringeren Synchronisierungsprobleme, der leichteren Anwendbarkeit des, ohne alternierende Richtungen arbeitenden, linieniterativen Lösungsverfahrens wurde für das hier behandelte Problem eine, aus maximal 26 Prozessoren bestehende, Ringstruktur gewählt, s. Abb. 5.1. Das Lösungsgebiet wird bei dieser Anordnung, wie in Abb. 5.2 gezeigt, in einzelne Streifen geteilt. Jeder Prozessor bearbeitet den ihm zugewiesenen Streifen. In dem in Abb. 5.2 dargestellten Ring bezeichnet M den Master-Prozessor; die Slave-Prozessoren sind mit den Symbolen Sj benannt.

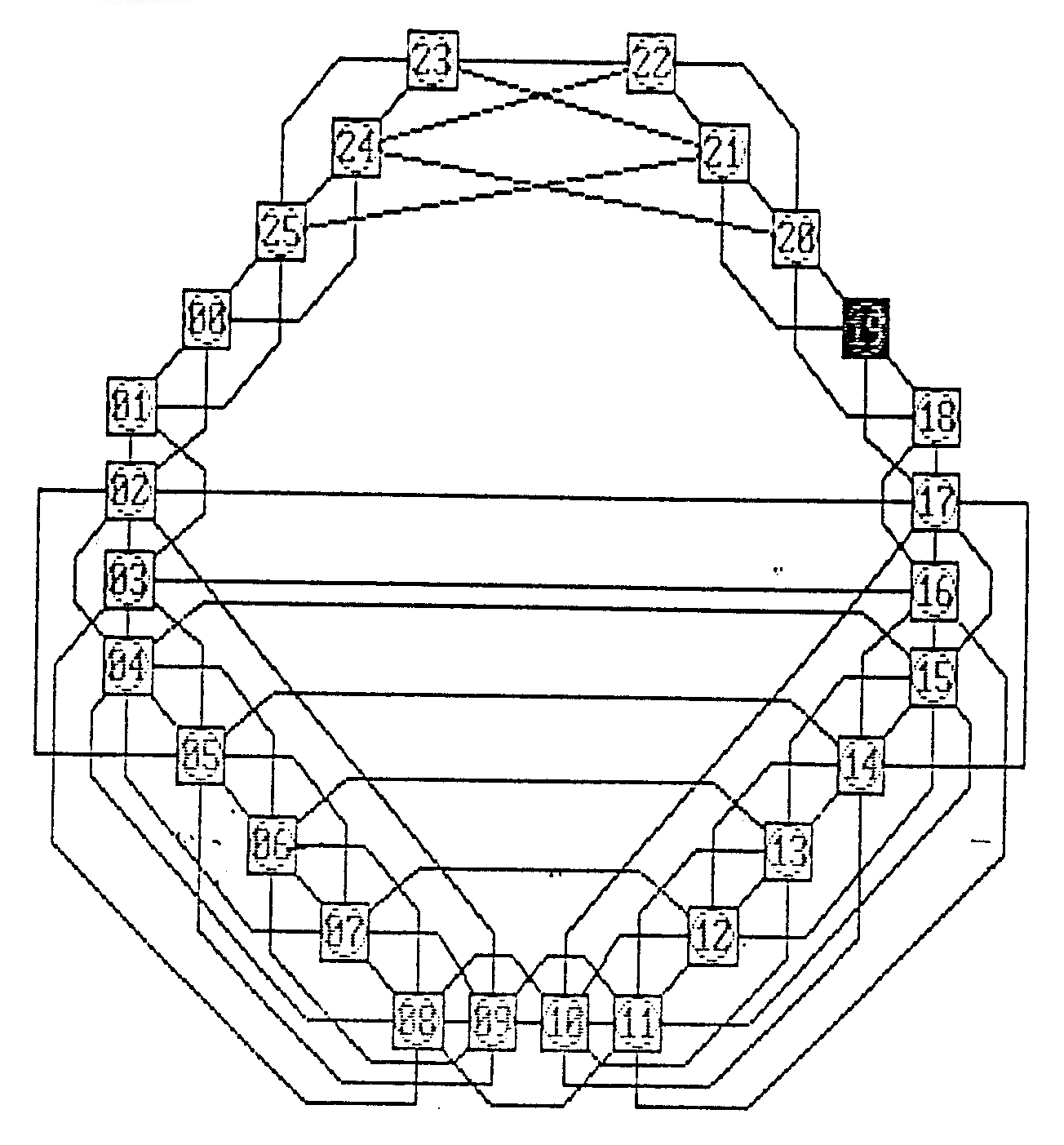
Abb. 5.1 : DIRMU-Ringkonfiguration

Prozessorring Lösungsgebiet

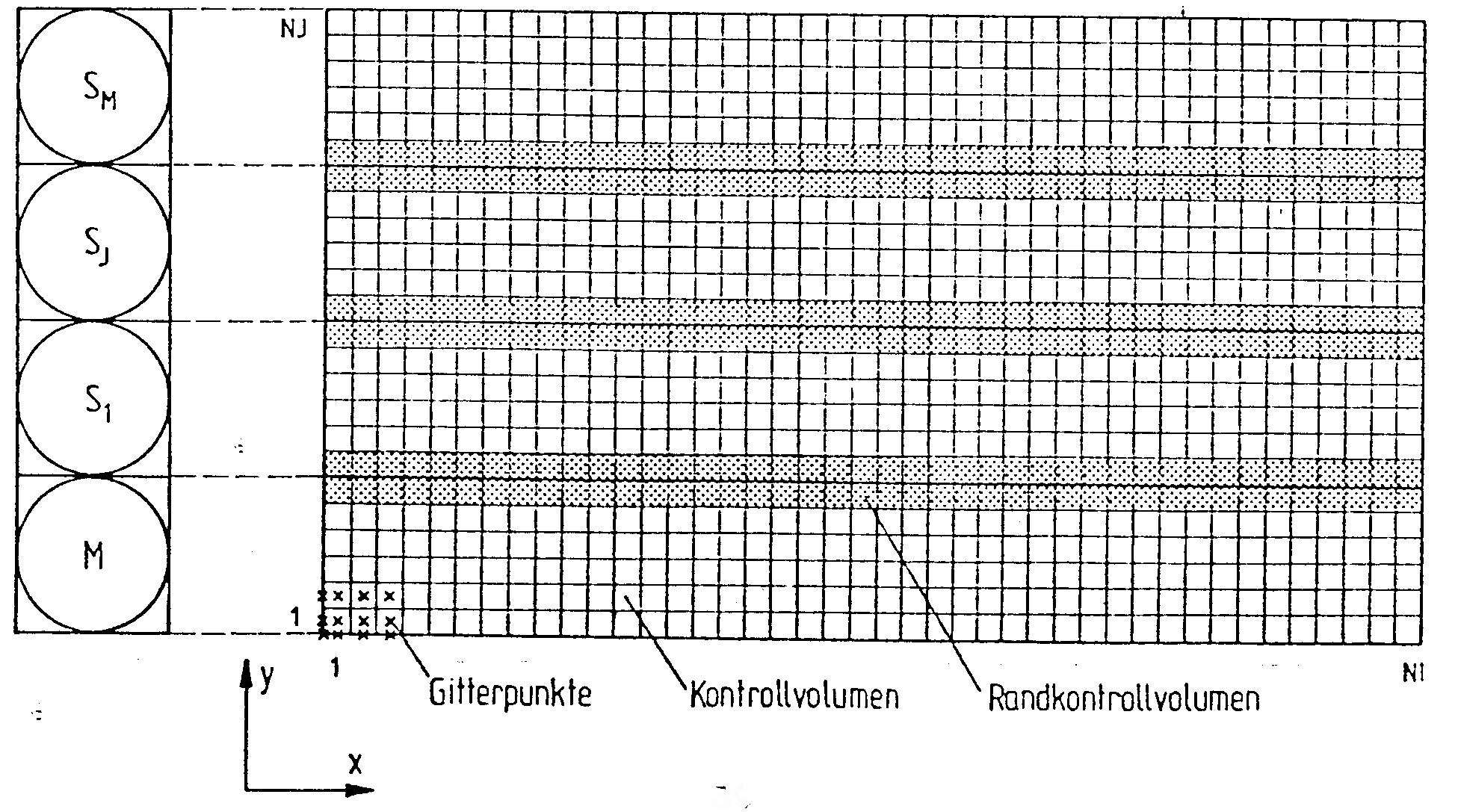
Abb. 5.2 : Aufteilung der Variablen

 

5.2 Aufteilung der Variablen

Im nächsten Schritt müßen die zu berechnenden Variablen auf die einzelnen Prozessoren verteilt werden. Die abhängigen Variablen des Problems sind die Geschwindigkeitsfelder [U] und [V] und das Druckfeld [P]. Diese sind in Vektoren der Länge NXY = NX*NY abgespeichert, wobei NX die Anzahl der Gitterpunkte in der xund NY die der y-Richtung bedeuten. Zu ihrer Berechnung werden zwölf weitere Vektoren der selben Länge für

• die Finiten-Volumen-Koeffizienten (Gl. (3.2-8)) 5
• die Massenströme Cx und Cy an den Kontrollvolumen grenzflächen 2
• das Druckkorrekturfeld [P‘] 1
• die Quellterme S und 2
• Hilfsfelder zur Berechnung der Koeffizienten in der Druckkorrekturgleichung (3. 3-10) 2

benötigt. Zusätzlich treten einige Vektoren der Länge NY auf, z.B. zur Speicherung der Flüsse an den Kontrollvolumenrändern, die jedoch vom Speicherplatzbedarf her nicht ins Gewicht fallen.

Bei der Aufteilung der Variablen werden die Begriffe lokale, regionale und globale Variablen benutzt. Sie sind wie folgt definiert:

• Lokale Variablen werden nicht von mehreren Prozessoren geteilt; sie stehen im Privatspeicher und werden vom Programm im Prozessor Sj (bzw. M) initialisiert.
• Regionale Variablen werden von Nachbarprozessoren geteilt. Sie stehen im Multiportspeicher.
• Globale Variable sind regionale Daten, die systemglobal gemacht werden. Sie befinden sich ebenfalls im Multiportspeicher.

Die oben erwähnten Felder der Länge NXY werden als regionale Variable behandelt. Wie in Abb. 5.2 gezeigt, wird in jedem Prozessor ein Streifen mit den Daten von NI und NJ/M Kontrollvolumen gespeichert. M ist die Anzahl der Prozessoren; die Anzahl der Kontrollvolumen errechnet sich zu NI = NX - 2 und NJ = NJ - 2. In den Prozessoren am oberen und unteren Integrationsrand ist jeweils eine zusätzliche Gitterpunktreihe gespeichert. Als globale Variable werden die zur Konvergenzabfrage notwendigen Summen der absoluten Residuen, der Massenstrom aus dem Integrationsgebiet und die Koordinaten einer Referenzstelle für den Druck behandelt.

In der vorliegenden Arbeit wurden die gesamten Teilfelder in den Multiportspeicher gelegt. Rein rechentechnisch wäre es effizienter, nur die Kontrollvolumenreihen an den Bereichsgrenzen der einzelnen Prozessoren im Multiport- und die inneren Reihen im Privatspeicher abzulegen (schraffierte Gebiete in Abb. 5.2). Dadurch können, speziell bei feinen Gittern, bei denen im Gegensatz zu Abb. 5.2 das Verhältnis aus der Anzahl der inneren Kontrollvolumenreihen zu den Randkontrollvolumenreihen groß ist, die zeitaufwendigeren Multiportspeicherzugriffe durch die schnelleren Privatspeicherzugriffe ersetzt werden. Gegen diese Maßnahme spricht, daß dadurch der Programmieraufwand erhöht bzw. die Transparenz eines parallelen Programmes deutlich vermindert wird (die Einheit "Teilmatrix" müßte in zwei regionale und ein globales Objekt aufgesplittet werden). Deshalb wurde hier darauf verzichtet. Ähnlich soll es auch in zukünftigen Erlanger Multiprozessorsystemen gemacht werden. Der Multiportspeicher wird im Vergleich zum Privatspeicher vergrössert, so daß alle derartigen Datenobjekte dort gespeichert werden können; der Privatspeicher enthält dann nur noch das Betriebssystem, das Anwenderprogramm und alle lokalen Datenobjekte.

Diese Arbeit besitzt eine Einschränkung, die wegen des Testcharakters des Programmes getroffen wurde. Im Master-Prozessor werden die gesamten Variablenfelder gespeichert und nach Beendigung der Rechnung gesammelt. Dadurch ist die Größe des maximal zu behandelnden Problems auf den Maximalspeicherplatz des Master-Prozessors beschränkt. Diese Limitierung wurde zur Erleichterung von Speedup- und Effizienzmessungen vorgenommen. Bei diesen Messungen wird das selbe Problem erst auf einem und dann auf mehreren Prozessoren gerechnet und die Rechenzeiten verglichen. Die Einschränkung in der zu behandelnden Problem-größe kann jedoch durch Änderungen bei der Initialisierung bzw. beim Output aufgehoben werden, so daß auch für praktische Anwendungen typische, wesentlich feinere, numerische Gitter bearbeitet werden können.

 

5.3. Ablauf des Verfahrens

Der erste Schritt beim Ablauf des Verfahrens ist die Initialisierung; die Geschwindigkeits- und Druckfelder in den einzelnen Prozessoren werden mit Schätzwerten vorbelegt und alle privaten und globalen Variablen entsprechend initialisiert. Dann läuft in jedem Prozessor das eigentliche Lösungsverfahren ab.

Zu Beginn werden die Finiten-Volumen-Koeffizienten und Quellterme der x-Impulsgleichung (3.3-1) berechnet. Dazu ist die Auswertung der konvektiven und diffusiven Flüße durch die Kontrollvolumengrenzflächen notwendig. In einer Schleife werden zuerst die Flüsse durch die West-Kontrollvolumengrenzflächen in allen Prozessoren ausgewertet. Für Interpolationsvorgänge an den Randkontrollvolumenreihen werden jeweils Werte vom Nachbar-prozessor geholt. In einer zweiten Schleife berechnen die Prozessoren die Flüsse durch die Süd-, Nord- und Ostseiten der ersten Kontrollvolumenspalte. Die Flüsse durch die Ostseiten werden in einem eindimensionalen Vektor der Länge NY gespeichert und als West-Flüsse für die nächste Kontrollvolumenspalte verwendet. An den übergangsstellen muß bei dem hier verwendeten konservativen Finiten-Volumen-Verfahren lediglich darauf geachtet werden, daß der Fluß durch die Nordseite des obersten Kontrollvolumens im S_j-Gebiet jeweils mit dem Fluß durch die Südseite des untersten Kontrollvolumens im S_j+1Gebiet identisch ist. Der geschilderte Ablauf wird für alle weiteren Kontrollvolumenspalten wiederholt. Die Koeffizientenberechnung ist in hohem Maße parallelisierbar, da keine Synchronisierungsvorgänge notwendig sind.

Nach der Berechnung der Koeffizienten gemäß den Gleichungen (3.2-8) werden die momentan im Speicher befindlichen Werte von [U] in die Finite-Volumen-Gleichung (3.3-1) eingesetzt und die Summe der absoluten Residuen nach der Beziehung (3.6-1) in allen Teilgebieten berechnet. Die für die einzelnen Gebiete resultierenden Werte werden bis zu einer Synchronisierungsrunde, die nach der Lösung der y-Impuls- und der Druckkorrekturgleichung erfolgt, zwischengespeichert.

Im Anschluß daran wird der in Abschnitt 3.5.1 beschriebene Lösungsalgorithmus aufgerufen. Die zur Parallelisierung dieses Verfahrens notwendigen Schritte werden gegen Ende dieses Abschnitts beschrieben.

Nach der (vorläufigen) Lösung des [U]-Feldes wird analog dazu das [V]-Feld bestimmt. Dann erfolgt eine Korrektur der Massen-flüsse am Austritt aus dem Lösungsgebiet; da das Verfahren konservativ ist, muß genau so viel Masse ein- wie ausfließen. Zur Realisierung dieser Bedingung wird der austretende Massenstrom gemäß

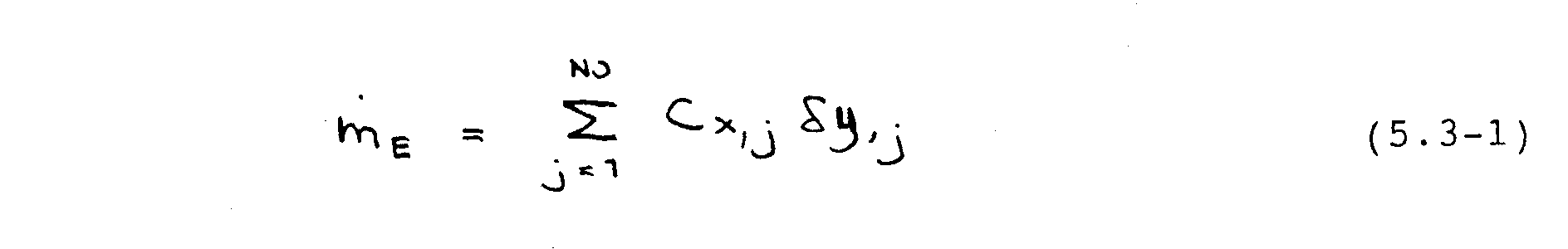
durch Auf summieren der Massenflüsse der einzelnen Kontrollvolumina an der Austrittsebene gebildet werden. Jeder Prozessor liefert zuerst den seinem Integrationsgebiet entsprechenden Teilmassenstrom, woraufhin eine globale Synchronisierung (s. Abschnitt 5.4) der Prozessoren zur Gesamtsummenbildung erfolgt Die Geschwindigkeiten am Austritt werden gemäß

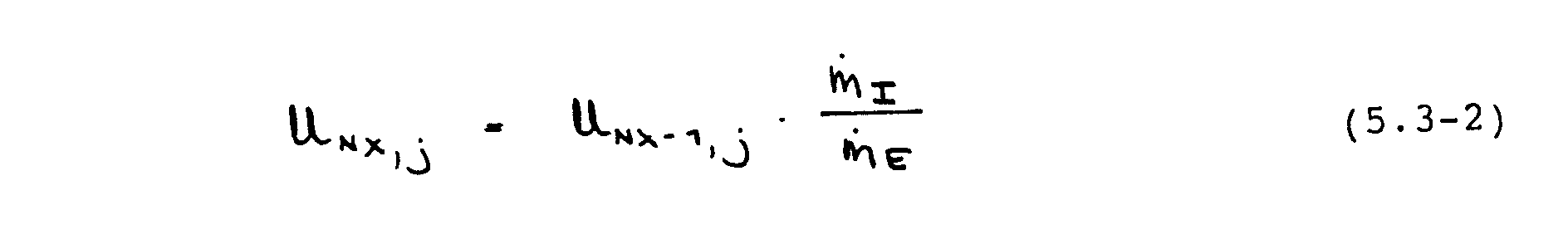
korrigiert.

 

Mit den vorliegenden Geschwindigkeitsfeldern werden die Massenströme C_x und C_y neu berechnet und der Quellterm für die Druckkorrekturgleichung (3.3-5) bestimmt. Simultan zu der Massenstrom- und Quelltermberechnung werden die Koeffizienten für die Druckkorrekturgleichung ermittelt. Die Koeffizienten für die Druckkorrekturgleichung sind symmetrisch, d.h. der Süd-Koeffizient der j-ten Kontrollvolumenzeile muß jeweils gleich dem Nord-Koeffizienten der (j-1)-ten Kontrollvolumenreihe sein. Bei der Berechnung der Koeffizienten für Kontrollvolumen an den Prozessorengrenzen muß dies entweder durch regionale Synchronisierung bzw. spezielle Programmierung (wie in dieser Arbeit) sichergestellt werden. Nach der Aufstellung der Koeffizienten wird das Massenresiduum als Summe der Absolutwerte der Quellterme S_m (Gl. (3.3-5)) berechnet und in allen Teilgebieten zwischengespeichert. Danach wird der Lösungsalgorithmus aufgerufen. Hier ist darauf zu achten, daß die Druckkorrekturgleichung relativ genau gelöst werden muß, da sonst unphysikalische Druckkorrekturen resultieren und das gesamte Verfahren u. U. divergiert.

Nach der Lösung der Druckkorrekturgleichung werden die Drücke und die Geschwindigkeiten mit den Beziehungen (3.3-3) korrigiert. Dies wird parallel in allen Teilgebieten durchgeführt. Damit ist eine vollständige Iteration des Verfahrens abgeschloßen. Es erfolgt eine globale Synchronisierung, in der die Teilsummen der zwischengespeicherten Residuumswerte für die U-, V- und Druckkorrekturgleichungen zu den jeweiligen, als globale Variable gespeicherten, Gesamtsummen aufaddiert werden. Diese werden mit dem vorgegebenen Abbruchkriterium verglichen. Falls der Maximalwert aus diesen drei Residuen größer als die Abbruchschranke ist, wird die beschriebene Prozedur mit den nunmehr im Speicher befindlichen Variablen wiederholt. Bei Unterschreiten des Abbruchkriteriums wird das Programm beendet. Der Master sendet eine Datensammel-Botschaft zu den Slaves, die daraufhin ihre [U]-, [V]- und [P]-Teilfelder an den Master senden, wo das Ergebnis zusammengesetzt und dann ausgegeben wird.

Zum Schluß dieses Abschnittes wird die parallele Implementierung des linieniterativen Lösungsalgorithmus besprochen. Wie bereits in Abschnitt 3.5.1 erwähnt, läuft der Algorithmus in zwei Durchgängen ab, wobei im ersten jeweils nur (aus der Vorschätzung oder von der vorhergehenden Iteration) bekannte Werte verwendet werden. Der erste Durchgang kann deshalb auf allen Prozessoren simultan, ohne Synchronisierung durchgeführt werden. Im zweiten Durchgang ist dagegen eine lokale Synchronisierung notwendig, da der Prozessor S_j+1 jeweils die Ergebnisse von Prozessor Sj benötigt und auf diese warten muß. Da jeweils nur entlang Linien mit y = const. direkt gelöst wird, ergibt sich bei der hier verwendeten Ringanordnung der Prozessoren ein relativ hoher Parallelisierungsgrad des linieniterativen Verfahrens.

 

5.4. Synchronisierung

Die Synchronisierung der Prozessoren ist ein sehr wichtiges Element bei der Entwicklung paralleler Algorithmen. Hier werden zwei Kategorien unterschieden, nämlich

 

• lokale Synchronisierung und
• globale Synchronisierung.

Bei lokaler Synchronisierung wird nur innerhalb der Nachbarschaft über gemeinsame Variablen synchronisiert. Jeder Prozessor wartet so lange mit der Fortsetzung seines Programmes, bis die Zustandsvariablen seiner Nachbarn die gewünschten Werte angenommen haben.

Globale Synchronisierung ist z.B. bei der Bildung der Summe der absoluten Residuen notwendig. Sie läuft folgendermaßen ab. Der Master legt seine Teilsumme im Speicher seines Nachbarn S₁ ab und setzt eine Boole‘sche Größe auf TRUE. Dies signalisiert S₁, daß die Teilsumme gültig ist. Er addiert nun seine Teilsumme zu diesem Wert, setzt die Boole‘sche Größe des Master zurück und gibt die neue Teilsumme genauso an S₂ weiter. In dieser Weise werden alle Prozessoren des Integrationsgebietes angesprochen. Der Master bekommt dann vom letzten Slave-Prozessor S_M ein Signal und liest die Summe der absoluten Residuen aus dem Multiportspeicher. Hierauf wird mit gleicher Mimik die Summe der absoluten Residuen durch den Ring hindurchgereicht. Falls die Residuen unterhalb der Abbruchschranke liegen, bedeutet dies für die Slaves geschickt, die Rechnung zu beenden.

Die für die globale Synchronisierung gewählte Methode hat den Nachteil hohen Zeitaufwandes für Ring-Konfigurationen mit vielen Prozessoren. In der vorliegenden DIRMU-Maschine mit 26 Prozessoren sind diese Zeitverluste noch nicht signifikant.

 

6. Ergebnisse

 

6.1. Strömungsfeld

Abbildung 6.1 zeigt die errechneten Geschwindigkeitsvektoren und Stromlinien. Die mit dem parallelisierten Programm auf DIRMU errechneten Geschwindigkeiten und Drücke wurden mit denen einer Berechnung auf einer seriellen Maschine (CDC CYBER 855 des Regionalen Rechenzentrums Erlangen) verglichen. Die Ergebnisse stimmten innerhalb der Zahlgenauigkeit der beiden Maschinen überein.

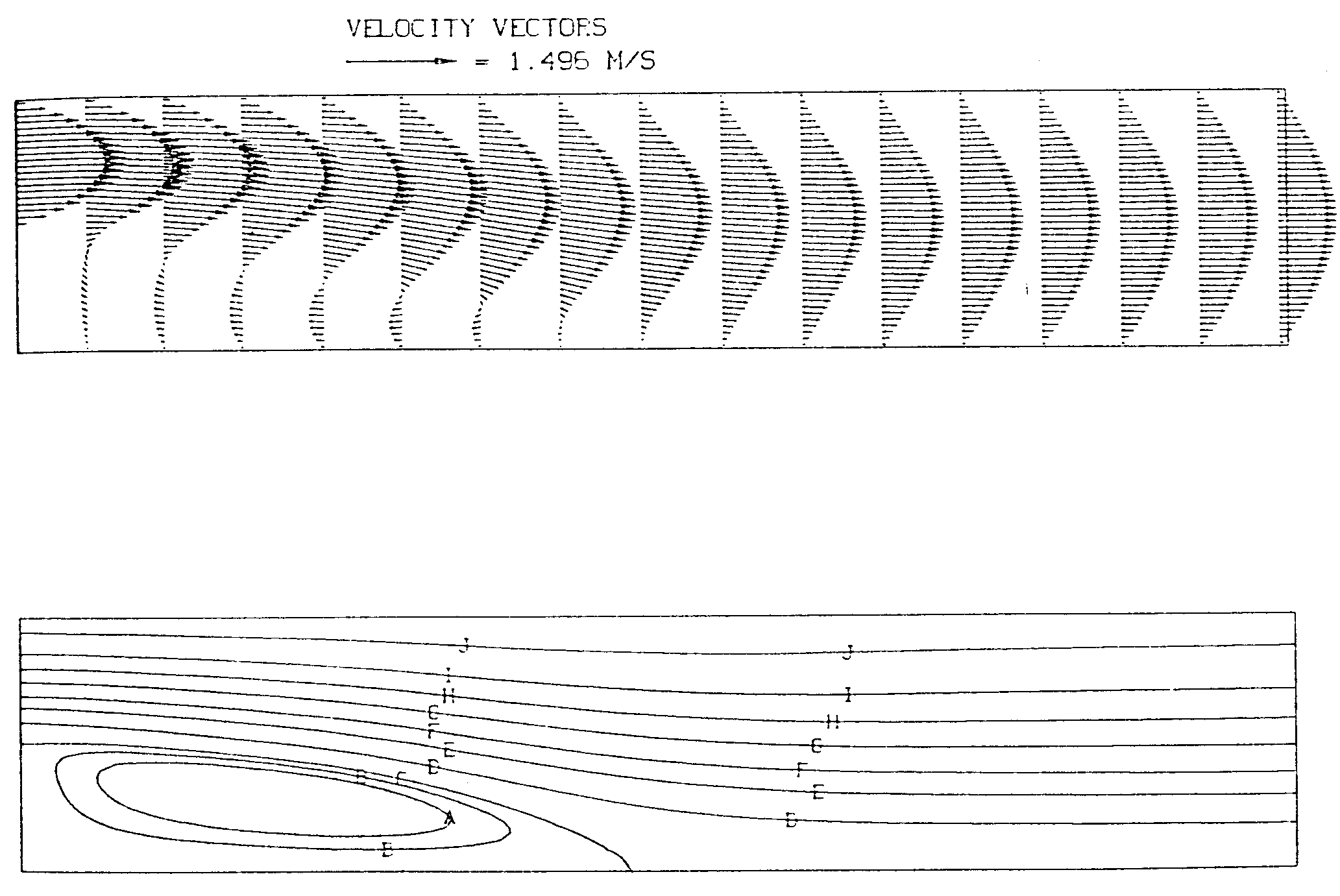
Abb. 6.1 Geschwindigkeitsvektoren und Stromlinien

 

6.2. Beschleunigung durch Parallelisierung

Rechenzeitmessungen wurden für zwei unterschiedliche numerische Gitter durchgeführt. Das erste bestand aus 20x10 Kontrollvolumen in der x- bzw. y-Richtung und das zweite aus 20x46 Kontrollvolumen. Die Rechenzeiten, Beschleunigungen (Speedup) und Effizienzen sind in den Tabellen 6-1 und 6-2 zusamnmengestellt. Zusätzlich sind die Speedup-Raten für die beiden Gitter in den Abbildungen 6.2 und 6.3 als Funktion der der Prozessorenanzahl dargestellt.

Anz. der Prozessoren	Anz. der Iterationen	Rechenzeit (s)	Speedup	Effiz. (%)
1	29	446.700	1.00	100
2	29	265.523	1.68	84
3	29	187.245	2.39	80
4	29	179.876	2.48	62
6	29	98.981	4.51	75

Tabelle 6-1 Ergebnisse für das 20x10 KV-Gitter

Der Speedup ist definiert als die Rechenzeit eines Prozessors geteilt durch die Rechenzeit von M Prozessoren. Die Effizienz ist das Verhältnis aus realem zu idealem Speedup. Der letztere ist gleich der Anzahl der Prozessoren.

Die beiden Tabellen zeigen, daß mit dem feineren numerischen Gitter natürlich bedeutend höhere Speedups bzw. Effizienzen als mit dem groben Gitter erzielt werden. Im Falle des feinen Gitters liegen die Effizienzen bei weniger als 12 Prozessoren über 90%.

Anz. der Prozessoren	Anz. der Iterationen	Rechenzeit (s)	Speedup	Effiz. (%)
2	235	8619.997	2.00	100.0
3	235	5828.656	2.96	98.6
4	235	4399.256	3.92	98.0
6	235	2962.094	5.82	97.0
8	235	2242.709	7.69	96.1
12	235	1523.944	11.31	94.3
16	235	1461.889	11.79	73.7
24	235	807.000	21.36	89.0

Tabelle 6-2 : Ergebnisse für das 20x46 KV-Gitter

Es wird also ein hoher Grad von Parallelität erzielt. Werden mehr als 12 Prozessoren verwendet, fallen die Effizienzen unter 90%. Die Ursache dafür ist, daß die von den einzelnen Prozessoren bearbeiteten Streifen immer schmaler werden und, im Verhältnis zur reinen Rechenzeit, mehr Synchronisierungszeit benötigt wird. Mit 24 Prozessoren wird jedoch immer noch ein Faktor von 21 an Rechenzeit gegenüber einem Prozessor eingespart.

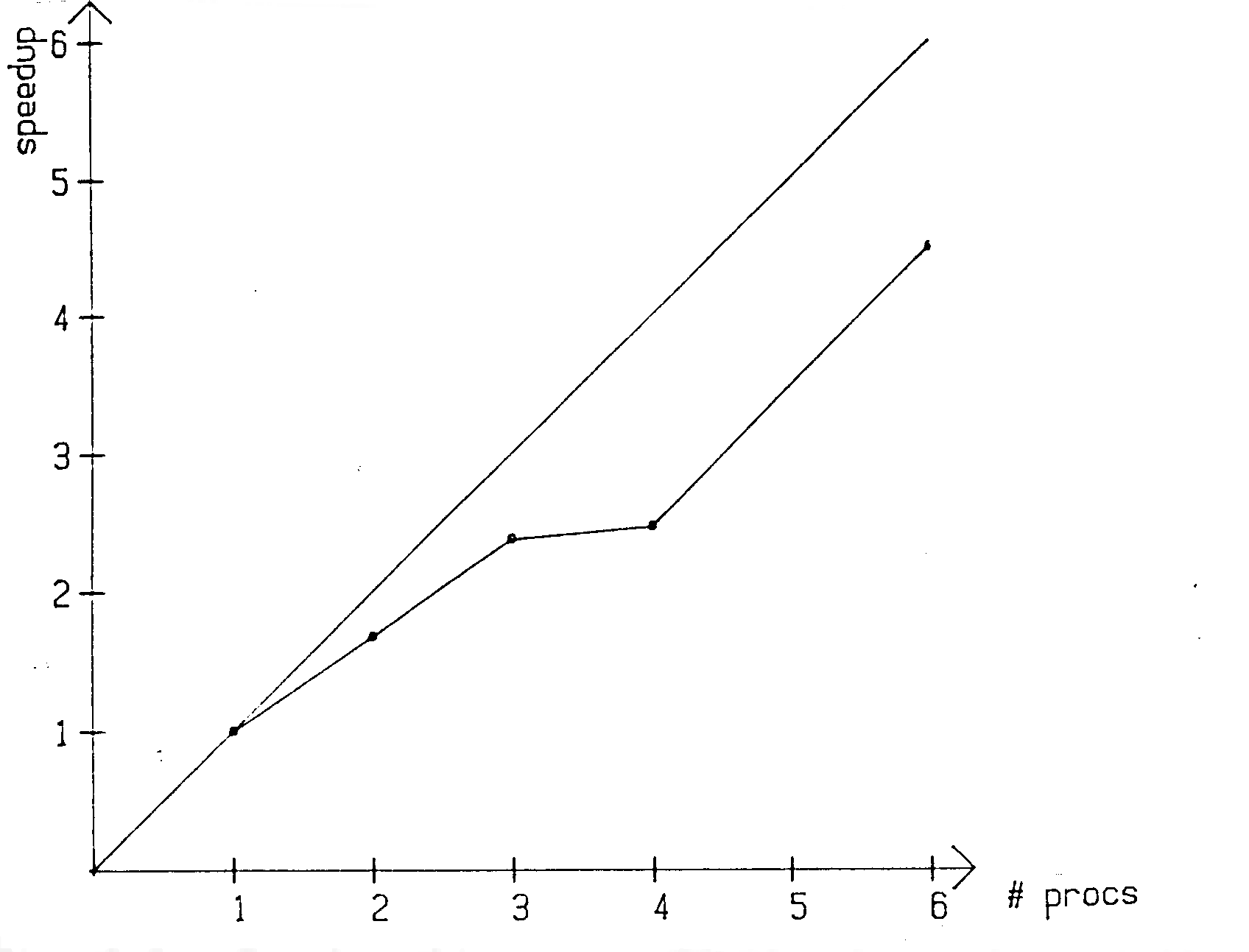
Abb. 6.2 : Speedup-Raten für das 20x10 KV-Gitter

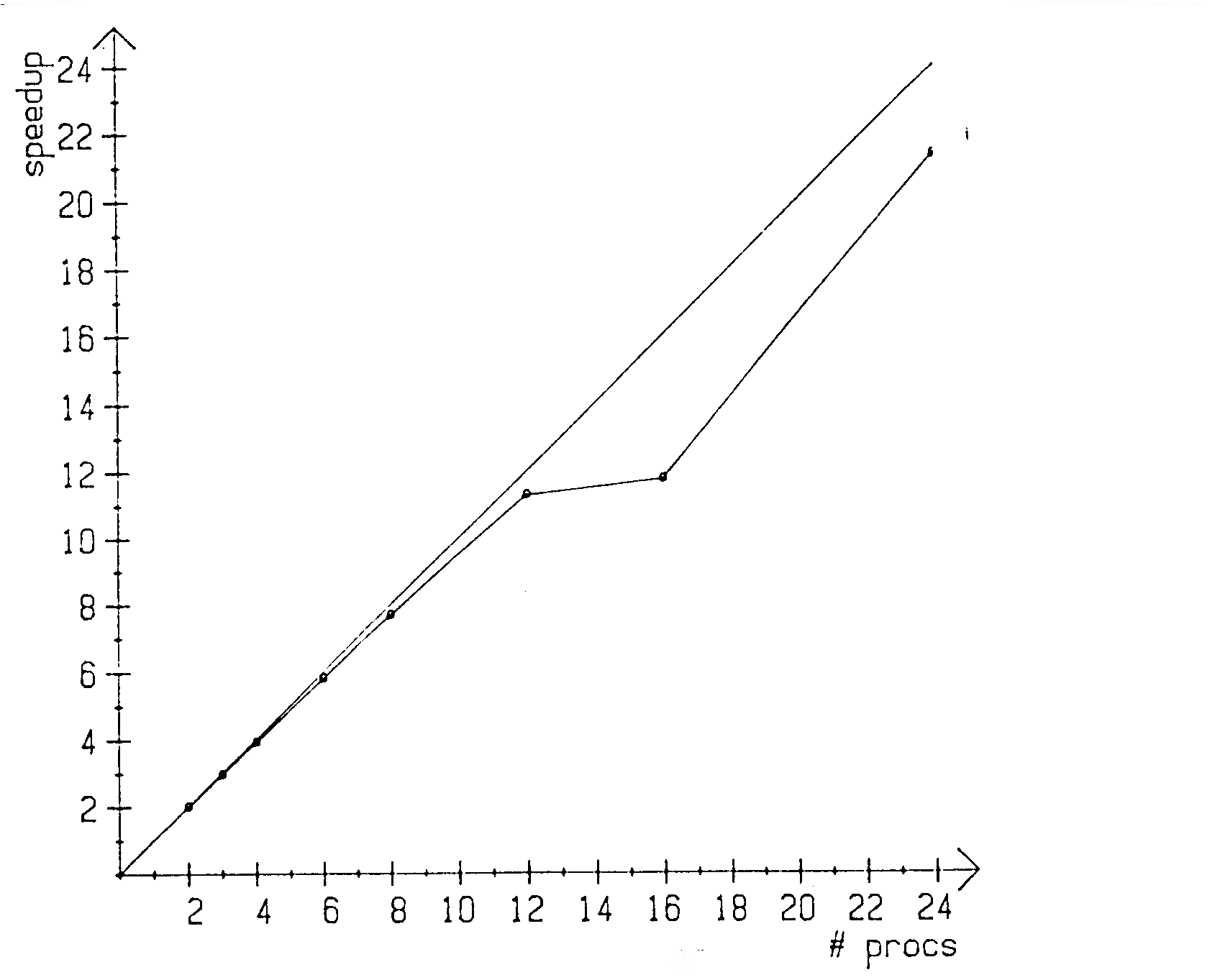
Abb. 6.3 : Speedup-Raten für das 20x46 KV-Gitter

Auf dem groben Gitter liegen die Effizienzen allesamt unter 90%; dies ist ebenfalls auf die, relativ gesehen, höheren Synchronisierungszeiten zurückzuführen. Die Knicke in den SpeedupRaten (z.B. beim Übergang von 12 auf 14 Prozessoren in Abb. 6.3) sind auf die dort auftretende, ungleichmäßigere Lastverteilung der Prozessoren zurückzuführen. Die Zahl der von den einzelnen Prozessoren zu bearbeitenden Kontrollvolumen ist unterschiedlich, so daß die mit weniger Last beaufschlagten Rechner jeweils auf die mehr arbeitenden warten müssen.

Die besten Effizienzen würden sich zweifelsohne ergeben, wenn der Maximalspeicherplatz jedes einzelnen Prozessors voll ausgenutzt würde. Die Synchronisierungszeiten werden dann gegenüber den Rechenzeiten klein und die Effizienzen steigen.

 

6.3. Diskussion und Verbesserungsvorschläge

In diesem Abschnitt werden einige Anmerkungen zur weiteren Optimierung des entwickelten Verfahrens gegeben.

 

6.3.1. Algorithmus

Der rechenzeitintensivste Teil in dem beschriebenen Verfahren ist der Lösungsalgorithmus. Im seriellen Rechenverfahren wird eine relativ effiziente Methode (Stone, 1968) benutzt, die auf einer unvollständigen LU-Zerlegung beruht. Diese Methode läßt sich nur unzureichend parallisieren. Die im parallelen Verfahren verwendeten Verfahren, wie der punktiterative Gauß-Seidel-Algorithmus bzw. das linieniterative Verfahren besitzen zwar einen hohen Grad an Parallelität, sind aber andererseits relativ ineffizient bei der Lösung großer Matrizen. Dies ist insbesondere ein Problem bei der Lösung der Druckkorrekturgleichung, die von Neumann-Randbedingungen an allen Rändern besitzt, und deren Konvergenz mit dem Gauß-Seidel-Verfahren für diesen Fall sehr schlecht ist. Auch der Einsatz des linieniterativen Verfahrens bringt hier keine entscheidenden Verbesserungen.

Langfristig ist es notwendig, effizientere Algorithmen mit höherem Parallelisierungsgrad zu entwickeln und zu erproben. Es sollte auch untersucht werden, inwieweit sich der Einsatz punktgekoppelter Verfahren auf Parallelrechnern auszahlt. Dies sind punktiterative Verfahren, bei denen für jedes Kontrollvolumen ein System für die Geschwindigkeitskomponenten und den Druck gelöst wird (Vanka, 1986). Zur weiteren Konvergenzbeschleunigung können diese Relaxationsverfahren in einen Mehrgitterzyklus eingebaut werden.

Die Koeffizientenberechnung und der linieniterative Lösungsalgorithmus lassen sich auf der Ring-Konfiguration sehr gut parallelisieren. Synchronisierung ist jeweils nur an einer "Nord-Süd"-Trennlinie notwendig. Bei einer Feld-Konfiguration sind im Gegensatz dazu Synchronisierungen an einer "Nord-Süd‘-und an einer "West-Ost"-Trennlinie nötig. Dadurch erhöht sich die reine Synchronisierungszeit (ohne Wartezeiten). Andererseits nimmt aber die Gesamtzahl der Kontrollvolumina, für die Synchronisierung durchgeführt werden muß, ab, wenn von einem Ring auf ein Feld übergegangen wird. Die Entscheidung für einen Ring bzw. für ein Feld hängt letztlich von der Größe des Problemes und der Anzahl der zur Verfügung stehenden Prozessoren ab. Bei einer großen Anzahl von Prozessoren sollte auf Felder übergegangen werden, da ansonsten der Synchronisierungs- aufwand bei Ringen (schmale Streifen; Synchronisierungssignale benötigen n Schritte im Gegensatz zu sqrt(n) bei Feldern) zu sehr ins Gewicht fällt.

Zeitverluste entstehen durch die notwendigen Synchronisierungsvorgänge. Globale Synchronisierungen benötigen zwei Runden durch den gesamten Ring: eine für die Berechnung der gesuchten globalen Größe und eine für die Weitergabe dieser Größe an alle Prozessoren. Die Synchronisierungsvorgänge müssen also auf ein Minimum beschränkt werden. Dies wurde in der vorliegenden Arbeit weitgehend realisiert. Teilweise kann Synchronisierung durch doppelte Berechnung gleicher Größen auf zwei benachbarten Prozessoren vermieden werden. Je nach Aufwand der arithmetischen Operationen für diese Doppelrechnung kann dies effizienter als eine Synchronisierung sein.

 

6.3.2. Hardware

Die DIRMU-Maschine wurde in den siebziger Jahren gebaut und ist mit den 8086/8087 Prozessoren mit einer Taktfrequenz von 5 MHz ausgestattet. Es ist klar, daß mit moderneren 32-Bit Prozessoren wesentlich höhere Leistungen zu erwarten sind. Besonders vielversprechend ist die Entwicklung mikroprogrammierbarer Koprozessoren, bei denen bestimmte, oft wiederkehrende Algorithmenteile (z.B. der Gauß-Seidel-Lösungsalgorithmus) vertikal, d.h. in Richtung der Firmware, verlagert werden. Dadurch laßen sich beträchtliche Rechenzeitgewinne erzielen.

 

7. Zusammenfassung und Schlußfolgerungen

In dieser Arbeit wurde eine Finite-Volumen-Methode zur Lösung der zweidimensionalen, inkompressiblen Navier-Stokes-Gleichungen parallelisiert und auf dem DIRMU-Multiprozessor-Systern implementiert. Als Rechnerkonfiguration wurde ein Ring gewählt; das Rechengebiet wurde in Streifen unterteilt, wobei jeder Prozessor einen solchen Streifen bearbeitet. Als Testfall wurde die laminare Strömung über eine rückwärts springende Stufe gewählt. Dafür lagen bereits Vergleichsrechnungen auf einer seriellen Maschine vor.

Die folgenden Schlußfolgerungen ergaben sich aus dieser Arbeit:

• Die verwendete Finite-Volumen-Methode läßt sich mit hoher Effizienz parallelisieren; bei einem numerischen Gitter mit 20x46 Kontrollvolumen in den beiden Raumrichtungen konnten bei Verwendung von 24 Prozessoren Rechenzeitgewinne um einen Faktor 21.4 erzielt werden. Die entsprechende Effizienz war 89%. Bei Verwendung von weniger Prozessoren steigen die Effizienzen (97 % bei 6 Prozessoren), da dann in den einzelnen Streifen des Rechengebietes der Rechenaufwand im Vergleich zu den notwendigen Synchronisierungen abnimmt. Wegen der speziellen, für Testzwecke ausgelegten Implementierung des Programmes konnten keine Berechnungen auf feineren Gittern durchgeführt werden.
• Die hohen Effizienzen dürfen jedoch nicht darüber hinwegtäuschen, daß wegen der Verwendung des punktiterativen Gauß-Seidel- bzw. des linieniterativen Lösungsalgorithmus in der parallelisierten Version wesentlich mehr innere Iterationen (Sweeps) benötigt werden, als in der zu Vergleichszwecken dienenden seriellen Version mit dem Lösungsalgorithmus von Stone (1968), der nur schlecht parallelisiert werden kann. Die Verwendung gut parallelisierbarer Lösungalgorithmen verschlechtert also die Effizienz des Gesamtverfahrens; es ist in jedem Falle abzuschätzen, ob die Gewinne durch Parallelisierung diese Verluste ausgleichen können. Andernfalls ist die Verwendung von Parallelrechnern nicht sinnvoll.

Aufgrund dieser Ergebnisse sollten zukünftig die folgenden Arbeiten angegangen werden:

• Systematische Erprobung und Test von verschiedenen Lösungsalgorithmen sowohl in Hinsicht auf Parallelisierbarkeit als auch auf Gesamtrechenzeit des Verfahrens.
• Einbindung des aus obiger Untersuchung als optimal erachteten Verfahrens in einen parallelisierten Mehrgitteralgorithmus zur Lösung der Navier-StokesGleichungen; diese Möglichkeit zur Konvergenzbeschleunigung sollte auf jeden Fall genutzt werden, um für die auf zukünftigen Parallelrechnern verwendeten feinen numerischen Gitter akzeptable Rechenzeiten zu erzielen.
• Kritischer Vergleich entkoppelter und gekoppelter Lösungsverfahren für die Navier-Stokes-Gleichungen auf Parallelrechnern. Der hier eingesetzte SIMPLEAlgorithmus ist ein entkoppeltes Verfahren: es werden sukzessive drei Matrizen für die beiden Geschwindkeiten und die Druckkorrektur gelöst. Bei den gekoppelten Verfahren wird eine Block-Matrix gelöst, d.h. für jedes Kontrollvolumen wird ein Gleichungssystem gelöst. Dadurch wird bei den gekoppelten Verfahren pro Kontrollvolumen mehr Rechenzeit relativ zu den Synchronisierungszeiten verbraucht, was die parallele Effizienz verbessern könnte. Diese Argumente müssen aber durch Versuche erhärtet werden.

 

8. Literatur

Barcus, M., 1987, "Berechnung zweidimensionaler Strömungsprobleme mit Mehrgitterverfahren", Diplomarbeit, Lehrstuhl für Strömungsmechanik, Universität Erlangen-Nürnberg.

Bird, R.B., Stewart, W.E., Lightfoot, E.N., 1960, ‘Transport Phenomena", J. Wiley & Sons Inc., New York.

Bradshaw, P., Cebeci, T., Whitelaw, J.H., 1981, "Engineering Calculation Methods for Turbulent Flow", Academic Press, London.

Geus, L., 1985, "Parallelisierung eines Mehrgitterverfahrens für die Navier-Stokes-Gleichungen auf EGPA-Systemen", Arbeitsberichte des Inst. f. Mathem. Maschinen und Datenverarbeitung, Universität Erlangen-Nürnberg, Band 18, Nummer 3.

Händler, W., Maehle, E., Wirl, K., 1985, "The DIRI4U Testbed for High-Performance Multiprocessor Configurations", Proc. of the First Intern. Conf. on Supercomputing Systems, St. Petersburg, FL, pp. 468—475.

Kutler, P., 1985, "A Perspective of Theoretical and Applied Computational Fluid Dynamics", AIAA-J., Vol. 23, pp. 328-341.

Maehle, E., Wirl, K., Japel, D., 1985, "Experiments with Parallel Programs on the DIRMU Multiprocessor", Parallel Computing, Berlin, pp. 515-520.

Patankar, S.V., 1980, "Numerical Heat Transfer and Fluid Flow", Hemisphere Publ. Corp., Washington.

Patankar, S.V., Spalding, D.B., 1972, "A Calculation Procedure for Heat, Mass and Momentum Transfer in Three—Dimensional Parabolic Flows‘, Int. J. Heat Mass Transfer, Vol. 15, pp. 1787—1806.

Peric, M., 1987, "Efficient Semi-Implicit Solving Algorithm for Nine-Diagonal Coefficient Matrix", Num. Heat Transfer, Vol. 11, pp. 251—279.

Peric, M., Scheuerer, G., 1987, "CAST - A Finite Volume Method for the Computer Simulation of Two-Dimensional Flows", Lehrstuhl f. Strömungsmechanik, Universität Erlangen-Nürbnerg, LSTM-Bericht 165/T/87.

Stone, H.L., 1968, "Iterative Solution of Implicit Approximations of Multidimensional Partial Differential Equations‘, SIAM J. Num. Anal., Vol. 5, pp. 530-558.

Thole, C.-A., 1985, "Experiments with Multigrid Methods on the CalTech-Hypercube" Gesellschaft f. Mathem. und Datenverarbeitung, St. Augustin, GMD-Studien Nr. 103.

Vanka, S.P., 1986, "Block-Implicit Multigrid Solution of Navier-Stokes Equations in Primitive Variables", J. Comp. Physics, Vol. 65, pp. 138—158.

Wirth, N., 1985, "Programming in MODULA-2", 3. ed., Springer Verlag, Berlin.